题目内容
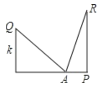
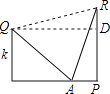
【题目】如图,设在一个宽度为w的小巷内,一个梯子长为a,梯子的脚位于A点,将梯子的顶端放在一堵墙上Q点时,Q离开地面的高度为k,梯子与地面的夹角为45°:将该梯子的顶端放在另一堵墙上R点时,R点离开地面的高度为h,且此时梯子与地面的夹角为75°,则小巷宽度w=( )
A.hB.kC.aD.![]()
【答案】A
【解析】
连接QR,过Q作QD⊥PR,则可证△AQR为等边三角形,得QR=AQ,进而求证△DQR≌△PRA,可得QD=RP,即墙面之间距离w=h.
解:连接QR,过Q作QD⊥PR,
∵Q离开地面的高度为k,梯子与地面的夹角为45°;
∴∠AQD=45°,
又∵R点离开地面的高度为h,且此时梯子与地面的夹角为75°
∴∠QAR=180°-75°-45°=60°,且AQ=AR,
∴△AQR为等边三角形,
即AQ=QR=AR,
∵∠AQD=45°
∴∠RQD=60°-45°=15°
∠ARP=90°-∠RAP=90°-75°=15°,
∴∠RQD=∠ARP
又∵∠QDR=∠P=90°,AR=QR
∴△DQR≌△PRA,
∴QD=PR,即w=h.
故选:A.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
【题目】用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素含量C及购这两种原料的价格如下表:
甲 | 乙 | |
维生素C(单位/千克) | 600 | 100 |
原料价格(元/千克) | 8 | 4 |
现配制这种饮料10千克,要求至少含有4200单位的维生素C,并要求购买甲、乙两种原料的费用不超过72元.请问:既要符合要求又要成本最低,则购买甲种原料应该在什么范围之内,最低成本是多少元?