Question

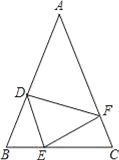
【题目】如图，在△ABC中，AB=AC，点D、E、F分别在BC、AB、AC边上，且BE=CF，AD+EC=AB．

（1）求证：△DEF是等腰三角形；

（2）当∠A=40°时，求∠DEF的度数；

（3）△DEF可能是等腰直角三角形吗？为什么？

（4）请你猜想：当∠A为多少度时，∠EDF+∠EFD=120°，并请说明理由．

Answer 1

【答案】（1）证明见解析；（2）∠DEF=70°； （3）△DEF不可能是等腰直角三角形，理由见解析；（4）当∠A=60°时，∠EDF+∠EFD=120°，理由见解析.

【解析】

（1）首先根据条件证明△DBE≌△ECF，根据全等三角形的性质可得DE=FE，进而可得到△DEF是等腰三角形；

（2）由（1）中的全等得出∠BDE=∠CEF，再由角之间的转化，从而可求解∠DEF的大小；（3）由于AB=AC，可得∠B=∠C≠90°=∠DEF，从而可确定其不可能是等腰直角三角形；

（4）先猜想出∠A的度数，则可得∠EDF+∠EFD=120°，根据前面的推导过程知∠EDF+∠EFD=120°时，∠DEF=60°，再由∠B=∠DEF以及等腰三角形的性质继而推得猜想的正确性.

（1）∵AB=AC，

∴∠B=∠C，

∵AD+EC=AB，AB=AD+BD，

∴BD=CE，

在△BDE和△CEF中，

，

∴△BDE≌△CEF（SAS）

∴DE=EF，

∴△DEF是等腰三角形；

（2）∵∠DEC=∠B+∠BDE，

即∠DEF+∠CEF=∠B+∠BDE，

由（1）知△BDE≌△CEF，

则∠BDE=∠CEF，

∴∠DEF=∠B，

∵∠A=40°，

∴∠B=∠C==70°，

∴∠DEF=70°；

（3）△DEF不可能是等腰直角三角形，

∵AB=AC，

∴∠B=∠C≠90°，

由（2）知∠DEF=∠B，

∴∠DEF=∠B≠90°，

∴△DEF不可能是等腰直角三角形；

（4）当∠A=60°时，∠EDF+∠EFD=120°，

理由是：当∠EDF+∠EFD=120°时，

则∠DEF=180°-120°=60°，

∴∠B=∠DEF=60°，

∴∠A=180°-∠B-∠C=180°-60°-60°=60°，

∴当∠A=60°时，∠EDF+∠EFD=120°.