题目内容
【题目】用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素含量C及购这两种原料的价格如下表:
甲 | 乙 | |
维生素C(单位/千克) | 600 | 100 |
原料价格(元/千克) | 8 | 4 |
现配制这种饮料10千克,要求至少含有4200单位的维生素C,并要求购买甲、乙两种原料的费用不超过72元.请问:既要符合要求又要成本最低,则购买甲种原料应该在什么范围之内,最低成本是多少元?
【答案】甲种材料在6.4≤x≤8范围之间,最低成本是65.6元.
【解析】
设所需甲种原料的质量为x千克,首先由甲种原料所需的质量和饮料的总质量,表示出乙种原料的质量,再结合表格中的数据,根据“至少含有4200单位的维生素C”这一不等关系列不等式,解不等式;然后根据购买甲、乙两种原料的费用不超过72元,可得甲种原料的取值范围,因为甲种原料每千克8元,乙种原料每千克4元,所以甲种原料尽量少时,最省钱.
解:设需用x千克甲种原料,则需乙种原料(10-x)千克,
依题意得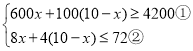
解①不等式,得,x≥6.4,
解②不等式,得x≤8,
∴不等式组的解集为:6.4≤x≤8.
又∵甲种原料每千克8元,乙种原料每千克4元,所以甲种原料尽量少时,最省钱
∴当甲需6.4千克,则乙需3.6千克,此时成本最低
最低成本为:6.4×8+3.6×4=65.6元
答:甲种材料在6.4≤x≤8范围之间,最低成本是65.6元.

 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案【题目】数学课上,李老师出示了如下框中的题目.
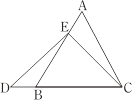
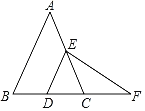
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图.试确定线段AE与DB的大小关系,并说明理由. |
|
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).

图1 图2
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).