Question

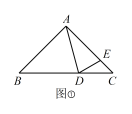
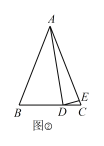
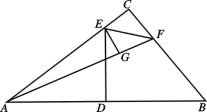
【题目】如图，在△ABC中，∠C＝90°，AB的垂直平分线DE交AC于点E，垂足是D，F是BC上一点，EF平分∠AFC，EG⊥AF于点G．

（1）试判断EC与EG，CF与GF是否相等；（直接写出结果，不要求证明）

（2）求证：AG＝BC；

（3）若AB＝5，AF+BF＝6，求EG的长．

Answer 1

【答案】（1）CE＝EG，CF=GF；（2）AG＝BC，见解析；（3）

【解析】

（1）根据角平分线性质得出EC＝EG，根据勾股定理推出CF＝GF即可．

（2）连接BE，推出AE＝BE，根据HL证出Rt△AGE≌Rt△BCE即可．

（3）求出BC，根据勾股定理求出AC，设EG＝EC＝x，则AE＝4﹣x，在Rt△AGE中，由勾股定理得出方程32+x2＝（4﹣x）2，求出方程的解即可．

（1）解：EC＝EG，CF＝GF，

理由是：∵∠C＝90°，EG⊥AF，EF平分∠AFC，且EF=EF

∴△ECF≌△EGF

∴CE＝EG，CF=GF．

（2）证明：连接BE，

∵AB的垂直平分线DE，

∴AE＝BE，

在Rt△AGE和Rt△BCE中，

，

∴Rt△AGE≌Rt△BCE（HL），

∴AG＝BC．

（3）解：∵AG＝BC＝BF+GF，

∴2AG＝AG+ BF+GF＝AF+ BF＝6 AG＝3

在Rt△ABC中，由勾股定理得：AC＝＝=4

设EG＝EC＝x，则AE＝4﹣x，在Rt△AGE中，

由勾股定理得：32+x2＝（4﹣x）2，

解得：x＝，

∴EG的长是