Question

【题目】在△ABC 中，AB=AC，点D 在底边BC 上，AE=AD，连接 DE．

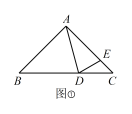
（1）如图①，已知∠BAC=90°，∠BAD=60°，求 ∠CDE 的度数；

（2）如图①，已知∠BAC=90°，当点D 在线段BC（点B，C 除外）上运动时，试探究∠BAD与 ∠CDE 的数量关系；

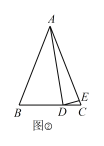
（3）如图②，若 ∠BAC≠90°，试探究∠BAD与 ∠CDE 的数量关系．

Answer 1

【答案】（1）∠CDE=30°；（2）∠CDE=∠BAD；（3）∠CDE=∠BAD.

【解析】

（1）根据等腰三角形的性质得到∠B=∠C=45°，由于AD=AE，于是得到∠AED=75°，根据三角形的外角性质即可得到∠CDE=75°-45°=30°；
（2）设∠BAD=x，于是得到∠CAD=90°-x，根据等腰三角形的性质得到∠AED=45°+ x，于是得到结论；
（3）设∠BAD=x，∠C=y，根据等腰三角形的性质得到∠BAC=180°-2y，由∠BAD=x，于是得到∠AED=y+ x，即可得到结论．

解：（1）∵AB=AC，∠BAC=90°，
∴∠B=∠C=45°，
∵∠BAD=60°，
∴∠DAE=30°，
∵AD=AE，
∴∠AED=75°，
∴∠CDE=∠AED-∠C=75°-45°=30°；
（2）∠CDE＝∠BAD；理由如下：

设∠BAD=x，
∴∠CAD=90°-x，
∵AE=AD，
∴∠AED=45°+ x，
∴∠CDE=∠AED-∠C=45°+ x -45° x，
即∠CDE＝∠BAD；
（3）∠CDE＝∠BAD；理由如下：

设∠BAD=x，∠C=y，
∵AB=AC，∠C=y，
∴∠BAC=180°-2y，
∵∠BAD=x，

∴∠CAD=180°-2y - x，

∵AD=AE，
∴∠AED= [180°-(180°-2y – x)] =y+ x，
∴∠CDE＝∠AED∠C＝y+ x - y =x．
即∠CDE＝∠BAD．