题目内容
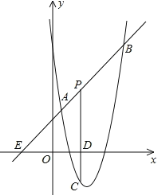
【题目】已知：如图（1），在平面直角坐标系中，点A、点B分別在x轴、y轴的正半轴上，点C在第一象限，∠ACB＝90°，AC＝BC，点A坐标为（m，0），点C横坐标为n，且m2+n2﹣2m﹣8n+17＝0．
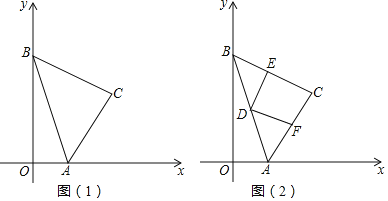
（1）分別求出点A、点B、点C的坐标；
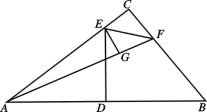
（2）如图（2），点D为边AB中点，以点D为顶点的直角∠EDF两边分别交边BC于E，交边AC于F，①求证：DE＝DF；②求证：S四边形DECF＝
S△ABC；
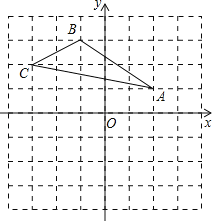
（3）在坐标平面内有点G（点G不与点A重合），使得△BCG是以BC为直角边的等腰直角三角形，请直接写出满足条件的点G的坐标．
【答案】（1）点A（1，0），点B（0，7），点C（4，4）；（2）①见解析；②见解析；（3）点G（-3，3）或（3，11）或（7，8）
【解析】
（1）由非负性可求m，n的值，由“AAS”可证△BCM≌△ACN，可得CM＝CN＝4＝OM，AN＝BM＝3，即可求解；
（2）①由等腰直角三角形的性质可得BD＝CD＝AD，∠ABC＝∠BAC＝∠BCD＝∠ACD＝45°，AB⊥CD，由“AAS”可证△BDE≌△CDF，可得DE＝DF；
②由全等三角形的性质可得S△BDE＝S△CDF，即可得结论；
（3）分三种情况讨论，由等腰直角三角形的性质和全等三角形的性质可求解．
（1）如图（1），过点C作CM⊥OB，CN⊥OA，
∵m2+n2﹣2m﹣8n+17＝0．
∴（m﹣1）2+（n﹣4）2＝0，
∴m＝1，n＝4，
∴点A（1，0），CM＝4，
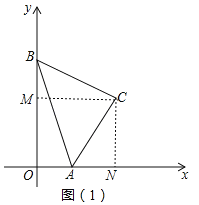
∵CM⊥OB，CN⊥OA，∠AOB＝90°，
∴四边形OMCN是矩形，
∴∠MCN＝90°＝∠ACB，CM＝ON＝4，CN＝OM，
∴AN＝3，∠MCN-∠MVA＝∠ACB-∠MVA
∴∠BCM＝∠ACN，
∵ AC＝BC，∠BMC＝∠ANC，
∴△BCM≌△ACN（AAS）
∴CM＝CN＝4＝OM，AN＝BM＝3，
∴点B（0，7），点C（4，4）；
（2）①如图（2），连接CD，
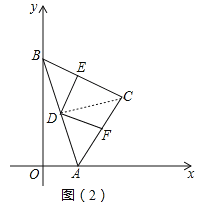
∵AC＝BC，∠ACB＝90°，点D为边AB中点，
∴BD＝CD＝AD，∠ABC＝∠BAC＝∠BCD＝∠ACD＝45°，AB⊥CD
∵∠EDF＝90°＝∠BDC，
∴∠EDF-∠EDC＝∠BDC-∠EDC
∴∠BDE＝∠CDF，
∵BD＝CD，∠ABC＝∠DCA，
∴△BDE≌△CDF（AAS）
∴DE＝DF，
②∵△BDE≌△CDF，
∴S△BDE＝S△CDF，
∴S△BDE+S△EDC＝S△CDF+S△EDC，
∴S△BDC＝S四边形EDFC，
∵AD＝BD，
∴
∴S四边形DECF＝
S△ABC；
（3）如图（3），
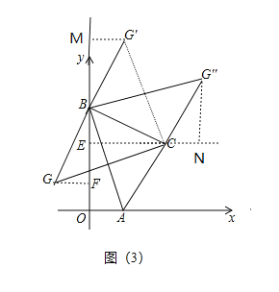
若∠GBC＝90°，BG＝BC时，且点G在BC下方，过点G作GF⊥OB，过点C作CE⊥OB，
∵∠GBF+∠EBC＝90°，∠GBF+∠BGF＝90°，
∴∠EBC＝∠BGF，
∵∠BEC＝∠BFG＝90°，BG＝BC，
∴△BGF≌△CBE（AAS）
∴BF＝CE＝4，GF＝BE，
∴OF＝OB-BF=7-4=3，
∴点G（﹣3，3），
若
时，且点
在BC上方，过点 作M⊥OB，过点C作CE⊥OB，
∵
∴
，
∵
∴
∴BM＝CE＝4，
，
∴OM＝OB+BM=7+4=11，
∴
，
若
，
时，点
在BC上方，过点 作N⊥EC，过点C作CE⊥OB，
∵
∴
，
∵
∴
∴CN＝BE＝3，
，
∴EN＝4+3=7，
∴点
综上所述：点G（﹣3，3）或G(3,11)或G(7,8)
