ЬтФПФкШн
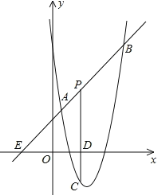
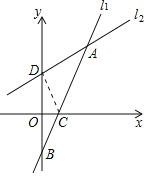
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌвбжЊжБЯпlЕФНтЮіЪНЮЊЃКyЃНkx+xЉk+1ЃЌШєНЋжБЯпlШЦAЕуа§зЊЃЎШчЭМЫљЪОЃЌЕБжБЯпlа§зЊЕНl1ЮЛжУЪБЃЌkЃН2Чвl1гыyжсНЛгкЕуBЃЌгыxжсНЛгкЕуCЃЛЕБжБЯпlа§зЊЕНl2ЮЛжУЪБЃЌkЃНЉ![]() Чвl2гыyжсНЛгкЕуD
Чвl2гыyжсНЛгкЕуD
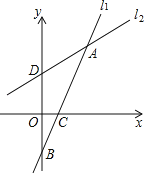
ЃЈ1ЃЉЧѓЕуAЕФзјБъЃЛ
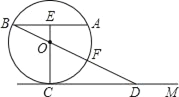
ЃЈ2ЃЉжБНгаДГіBЁЂCЁЂDШ§ЕуЕФзјБъЃЌСЌНгCDМЦЫуЁїADCЕФУцЛ§ЃЛ
ЃЈ3ЃЉвбжЊзјБъЦНУцФквЛЕуEЃЌЦфзјБъТњзуЬѕМўEЃЈaЃЌaЃЉЃЌЕБЕуEгыЕуAОрРызюаЁЪБЃЌжБНгаДГіaЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉAЕуЕФзјБъЮЊЃЈ1ЃЌ2ЃЉЃЛЃЈ2ЃЉBЃЈ0ЃЌЉ1ЃЉЁЂCЃЈ![]() ЃЌ0ЃЉЁЂDЃЈ0ЃЌ
ЃЌ0ЃЉЁЂDЃЈ0ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ![]() ЃЛЃЈ3ЃЉaЃН
ЃЛЃЈ3ЃЉaЃН![]()
ЁОНтЮіЁП
ЃЈ1ЃЉНЋkЃН2КЭkЃН![]() ДњШыжБЯпЕФНтЮіЪНЃЌЕУЕНЙигкxЁЂyЕФЗНГЬзщЃЌШЛКѓНтЗНГЬзщПЩЧѓЕУЕуAЕФзјБъЃЛ
ДњШыжБЯпЕФНтЮіЪНЃЌЕУЕНЙигкxЁЂyЕФЗНГЬзщЃЌШЛКѓНтЗНГЬзщПЩЧѓЕУЕуAЕФзјБъЃЛ
ЃЈ2ЃЉСЌНгDCЃЎЯШЧѓЕУЕуBЁЂCЁЂDЕФзјБъЃЌШЛКѓвРОнSЁїADCЃНSЁїADBЉSЁїBDCЧѓНтМДПЩЃЛ
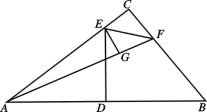
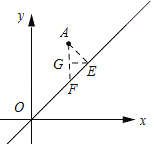
ЃЈ3ЃЉЙ§ЕуAзїжБЯпyЃНxЕФДЙЯпЃЌДЙзуЮЊEЃЌЙ§ЕуAзїAFЁЮyжсЃЌЙ§ЕуEзїEGЁЭAFЃЌДЙзуЮЊGЃЎЯШЧѓЕУAFЕФжЕЃЌШЛКѓгЩЁїAEFЮЊЕШбќжБНЧШ§НЧаЮЃЌДгЖјПЩЧѓЕУЕуEЕФзјБъЃЌЙЪДЫПЩЕУЕНaЕФжЕЃЎ
ЃЈ1ЃЉЕБkЃН2ЪБЃЌyЃН3xЉ1ЃЌ
ЕБkЃНЉ![]() ЪБЃЌyЃН
ЪБЃЌyЃН![]() x+
x+![]() ЃЎ
ЃЎ
НтЗНГЬзщЃЌ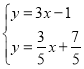
ЕУЃК![]() ЃЌ
ЃЌ
ЁрAЕуЕФзјБъЮЊЃЈ1ЃЌ2ЃЉЃЎ
ЃЈ2ЃЉСЌНгDCЃЎ
НЋxЃН0ДњШыyЃН3xЉ1ЕУЃКyЃНЉ1ЃЌ
ЁрBЃЈ0ЃЌЉ1ЃЉЃЎ
НЋyЃН0ДњШыyЃН3xЉ1ЕУЃК3xЉ1ЃН0ЃЌНтЕУЃКxЃН![]() ЃЎ
ЃЎ
ЁрCЃЈ![]() ЃЌ0ЃЉЃЎ
ЃЌ0ЃЉЃЎ
НЋxЃН0ДњШыyЃН![]() x+
x+![]() ЕУЃКyЃН
ЕУЃКyЃН![]() ЃЌ
ЃЌ
ЁрDЃЈ0ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁрBDЃН![]() ЃЌOCЃН
ЃЌOCЃН![]() ЃЎ
ЃЎ
ЁрSЁїADCЃНSЁїADBЉSЁїBDCЃН![]() ЁС
ЁС![]() ЁС1Љ
ЁС1Љ![]() ЁС
ЁС![]() ЃЎ
ЃЎ
ЃЈ3ЃЉЁпEЃЈaЃЌaЃЉЃЌ
ЁрЕуEдкжБЯпyЃНxЩЯЃЎ
ШчЭМЫљЪОЃКЙ§ЕуAзїжБЯпyЃНxЕФДЙЯпЃЌДЙзуЮЊEЃЌЙ§ЕуAзїAFЁЮyжсЃЌЙ§ЕуEзїEGЁЭAFЃЌДЙзуЮЊGЃЎ
НЋxЃН1ДњШыyЃНxЕУЃКyЃН1ЃЌ
ЁрAFЃН2Љ1ЃН1ЃЎ
ЁпЕуEдкжБЯпyЃНxЩЯЃЌ
ЁрЁЯAFEЃН45ЁуЃЌ
ЁрЁїAEFЮЊЕШбќжБНЧШ§НЧаЮЃЎ
ЁпEGЁЭAFЃЌ
ЁрAGЃНFGЃН![]() ЃЌ
ЃЌ
ЁрEЕФзнзјБъЃН1+![]() ЃН
ЃН![]() ЃЎ
ЃЎ
ЁрaЃН![]() ЃЎ
ЃЎ