题目内容
【题目】下列因式分解正确的是( )
A.(x+5)(x-3)=x2+2x-15B.2x2-4x-1=2x(x-2)-1
C.x2y-2xy2+xy=xy(x-2y)D.x3-9x=x(x+3)(x-3)
【答案】D
【解析】
利用因式分解的定义对A、B进行判断;根据提公因式法对C进行判断;根据提公因式和运用公式法对D进行判断.
A.(x+5)(x-3)=x2+2x-15,是整式乘法,不是因式分解,故A错误;
B.2x2-4x-1=2x(x-2)-1,不是因式分解,故B错误;
C.x2y-2xy2+xy=xy(x-2y+1),故C错误;
D.x3-9x=x(x2-9)=x(x+3)(x-3),故D正确.
故选:D.

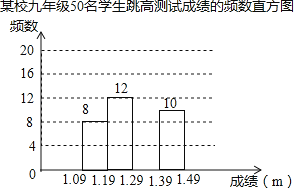
【题目】为了了解某校九年级学生的跳高水平,随机抽取该年级50名学生进行跳高测试,并把测试成绩绘制成如图所示的频数表和未完成的频数直方图(每组含前一个边界值,不含后一个边界值).
某校九年级50名学生跳高测试成绩的频数表
组别(m) | 频数 |
1.09~1.19 | 8 |
1.19~1.29 | 12 |
1.29~1.39 | A |
1.39~1.49 | 10 |
(1)求a的值,并把频数直方图补充完整;
(2)该年级共有500名学生,估计该年级学生跳高成绩在1.29m(含1.29m)以上的人数.
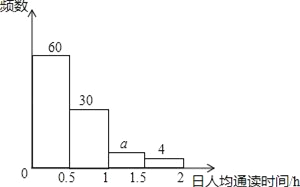
【题目】某校1200名学生参加了全区组织的“经典诵读”活动,该校随机选取部分学生,对他们在三、四两个月的诵读时间进行调查,下面是根据调查数据制作的统计图表的一部分.
根据以上信息,解答下列问题:
(1)本次调查的学生数为__人;
(2)图表中的a、b、c的值分别为__,__,__;
(3)在被调查的学生中,四月份日人均诵读时间在1<x≤1.5范围内的人数比三月份在此范围的人数多__人;
(4)试估计该校学生四月份人均诵读时间在1小时以上的人数.
四月日人均诵读时间的统计表
日人均诵读时间x/h | 人数 | 百分比 |
0≤x≤0.5 | 6 | |
0.5<x≤1 | 30 | |
1<x≤1.5 | 50% | |
1.5<x≤2 | 10 | 10% |
2<x≤2.5 | b | c |
三月日人均诵读时间的频数分布直方图