��Ŀ����
����Ŀ��ijУ1200��ѧ���μ���ȫ����֯���������ж��������У���ѡȡ����ѧ�����������������������µ��ж�ʱ����е��飬�����Ǹ��ݵ�������������ͳ��ͼ����һ���֣�
����������Ϣ������������⣺
��1�����ε����ѧ����Ϊ__�ˣ�
��2��ͼ���е�a��b��c��ֵ�ֱ�Ϊ__��__��__��
��3���ڱ������ѧ���У����·����˾��ж�ʱ����1��x��1.5��Χ�ڵ����������·��ڴ˷�Χ��������__�ˣ�
��4���Թ��Ƹ�Уѧ�����·��˾��ж�ʱ����1Сʱ���ϵ�������
�������˾��ж�ʱ���ͳ�Ʊ�
���˾��ж�ʱ��x/h | ���� | �ٷֱ� |
0��x��0.5 | 6 | |
0.5��x��1 | 30 | |
1��x��1.5 | 50% | |
1.5��x��2 | 10 | 10% |
2��x��2.5 | b | c |
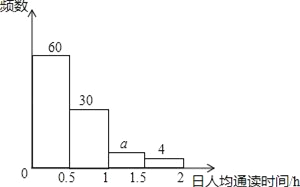
�������˾��ж�ʱ���Ƶ���ֲ�ֱ��ͼ
���𰸡� 100 2 4 4% 44
�������������������1����ͳ�Ʊ����Եõ����ε����ѧ������
��2����ͳ��ͼ��ͳ�Ʊ����Էֱ����a��b��c��ֵ��
��3����ͳ��ͼ��ͳ�Ʊ�����������·����˾��ж�ʱ����1��x��1.5��Χ�ڵ����������·��ڴ˷�Χ������������ˣ�
��4������ͳ�Ʊ�������ø�Уѧ�����·��˾��ж�ʱ����1Сʱ���ϵ�������
����������⣺��1����ͳ�Ʊ��ɵã�
���ε����ѧ����Ϊ��10��10%=100��
�ʴ�Ϊ��100��
��2��������ͳ��ͼ�ɵã�a=100��60��30��4=6��
��ͳ�Ʊ��ɵã�b=100��6��30��100��50%��10=4��c=4��100=4%��
�ʴ�Ϊ��6��4��4%��
��3����ͳ�Ʊ��ɵã����·����˾��ж�ʱ����1��x��1.5��Χ�ڵ������У�100��50%=50���ˣ���
��Ƶ���ֲ�ֱ��ͼ�ã����·����˾��ж�ʱ����1��x��1.5��Χ�ڵ�������6���ˣ���
�����·����˾��ж�ʱ����1��x��1.5��Χ�ڵ����������·��ڴ˷�Χ�������ࣺ50��4=44���ˣ���
�ʴ�Ϊ��44��
��4����ͳ�Ʊ��ɵã�
�Ƹ�Уѧ�����·��˾��ж�ʱ����1Сʱ���ϵ������У�1200����50%+10%+4%��=768���ˣ���
���Ƹ�Уѧ�����·��˾��ж�ʱ����1Сʱ���ϵ�������768�ˣ�