题目内容
已知:如图,一次函数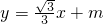 与反比例函数
与反比例函数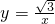 的图象在第一象限的交点为A(
的图象在第一象限的交点为A( 1,n).
1,n).
(1)求m与n的值;
(2)设一次函数的图象与x轴交于点B,连接OA,求∠BAO的度数.
解:(1)∵点A(1,n)在双曲线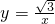 上,
上,
∴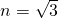 ,
,
又∵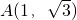 在直线
在直线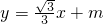 上,
上,
∴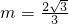 ;
;
(2)过点A作AM⊥x轴于点M.
∵直线 与x轴交于点B,
与x轴交于点B,
∴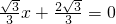 ,
,
解得x=-2.
∴点B的坐标为(-2,0),
∴OB=2.
∵点A的坐标为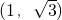 ,
,
∴ .
.
在Rt△AOM中,∠AMO=90°,
∴tan ,
,
∴∠AOM=60°.
由勾股定理,得OA=2.
∴OA=OB,
∴∠OBA=∠BAO,
∴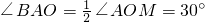 .
.
分析:(1)把A(1,n)代入反比例函数的解析式即可求出n的值即得A点坐标,再把A点坐标代入一次函数的解析式便可求出m的值;
(2)过点A作AM⊥x轴于点M,根据一次函数的解析式可求出B点坐标,由A点坐标可求出∠AOM的度数,由勾股定理可求出OA的长,判断出△OAB的形状,再根据特殊角的三角函数值即可求出∠OBA的度数,进而求出∠BAO的度数.
点评:本题考查的是反比例函数及一次函数图象上点的坐标特点,特殊角的三角函数值及等腰三角形的性质,涉及面较广,但难度适中.
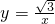 上,
上,∴
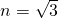 ,
,又∵
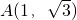 在直线
在直线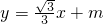 上,
上,∴
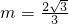 ;
;(2)过点A作AM⊥x轴于点M.

∵直线
 与x轴交于点B,
与x轴交于点B,∴
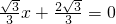 ,
,解得x=-2.
∴点B的坐标为(-2,0),
∴OB=2.
∵点A的坐标为
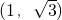 ,
,∴
 .
.在Rt△AOM中,∠AMO=90°,
∴tan
 ,
,∴∠AOM=60°.
由勾股定理,得OA=2.
∴OA=OB,
∴∠OBA=∠BAO,
∴
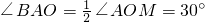 .
. 分析:(1)把A(1,n)代入反比例函数的解析式即可求出n的值即得A点坐标,再把A点坐标代入一次函数的解析式便可求出m的值;
(2)过点A作AM⊥x轴于点M,根据一次函数的解析式可求出B点坐标,由A点坐标可求出∠AOM的度数,由勾股定理可求出OA的长,判断出△OAB的形状,再根据特殊角的三角函数值即可求出∠OBA的度数,进而求出∠BAO的度数.
点评:本题考查的是反比例函数及一次函数图象上点的坐标特点,特殊角的三角函数值及等腰三角形的性质,涉及面较广,但难度适中.

练习册系列答案
相关题目
 知
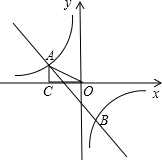
知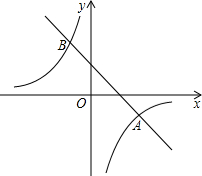 (2013•白云区一模)已知,如图,一次函数y=kx+b的图象与反比例函数y=
(2013•白云区一模)已知,如图,一次函数y=kx+b的图象与反比例函数y=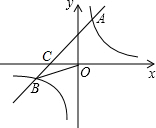 已知:如图,一次函数y=kx+b的图象与反比例函数
已知:如图,一次函数y=kx+b的图象与反比例函数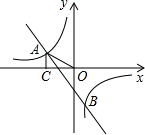 OA=
OA=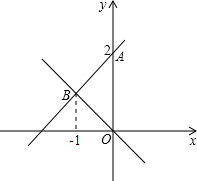 已知:如图,一次函数y=kx+b的图象与y轴交于点A,且与正比例函数y=-x的图象交于点B,则该一次函数的解析式为
已知:如图,一次函数y=kx+b的图象与y轴交于点A,且与正比例函数y=-x的图象交于点B,则该一次函数的解析式为