题目内容
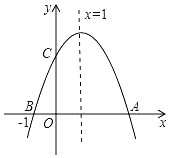
【题目】如图,二次函数y=ax2+bx+c(a≠0)图象与x轴交于A,B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0).则下面的四个结论:
①abc>0;②8a+c<0;③b2﹣4ac>0;④当y<0时,x<﹣1或x>2.
其中正确的有( )
A.4个B.3个C.2个D.1个
【答案】C
【解析】
根据二次函数的图象和二次函数的性质,可以判断各个小题中的结论是否成立,从而可以解答本题.
①函数的对称轴在y轴右侧,则ab<0,而c>0,故abc<0,故原答案错误,不符合题意;
②函数的对称轴为:x![]() 1,故b=﹣2a,对称轴为x=1,点B坐标为(﹣1,0),则点A(3,0),故9a+3b+c=0,而b=﹣2a,即3a+c=0,a<0,故8a+c<0,正确,符合题意;
1,故b=﹣2a,对称轴为x=1,点B坐标为(﹣1,0),则点A(3,0),故9a+3b+c=0,而b=﹣2a,即3a+c=0,a<0,故8a+c<0,正确,符合题意;
③抛物线和x轴有两个交点,故b2﹣4ac>0正确,符合题意;
④点B坐标为(﹣1,0),点A(3,0),则当y<0时,x<﹣1或x>3.故错误,不符合题意.
故选:C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某数学“综合与实践”小组的同学把“测量大桥斜拉索顶端到桥面的距离”作为一项课题活动,他们制订了测量方案,并利用课余时间借助该桥斜拉索完成了实地测量.测量结果如下表.
项目 | 内容 | ||
课题 | 测量斜拉索顶端到桥面的距离 | ||
测量示意图 |
| 说明:大桥两侧一组斜拉索AC,BC相交于点C,分别与桥面交于A,B两点,且点A,B,C在同一竖直平面内. | |
测量数据 | ∠A的度数 | ∠B的度数 | AB的长度 |
45° | 30° | 240米 | |
… | … | ||
请帮助该小组根据上表中的测量数据,求斜拉索顶端点C到AB的距离.(结果精确到0.1米)(参考数据:![]() =1.414,
=1.414,![]() =1.732)
=1.732)