ΧβΡΩΡΎ»ί
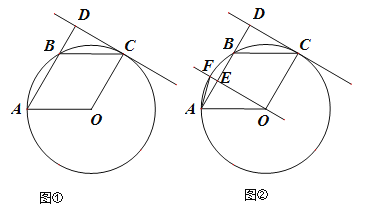
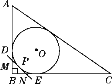
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΥΡ±Ώ–ΈABCD÷–Θ§ADΓΈBCΘ§ΓœABCΘΫ90ΓψΘ§ABΘΫ12 cmΘ§ADΘΫ8 cmΘ§BCΘΫ22 cmΘ§ABΈΣΓ―OΒΡ÷±ΨΕΘ§Ε·ΒψP¥”ΒψAΩΣ Φ―ΊAD±ΏœρΒψD“‘1 cm/sΒΡΥΌΕ»‘ΥΕ·Θ§Ε·ΒψQ¥”ΒψCΩΣ Φ―ΊCB±ΏœρΒψB“‘2 cm/sΒΡΥΌΕ»‘ΥΕ·Θ§PΘ§QΖ÷±π¥”ΒψAΘ§CΆ§ ±≥ωΖΔΘ°Β±Τδ÷–“ΜΕ·ΒψΒΫ¥ο÷’Βψ ±Θ§Νμ“ΜΗωΕ·Βψ“≤Υφ÷°ΆΘ÷Ι‘ΥΕ·Θ°…η‘ΥΕ· ±ΦδΈΣt sΘ°Β±tΈΣΚΈ÷Β ±Θ§PQ”κΓ―Oœύ«–ΘΩ
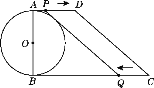
ΓΨ¥πΑΗΓΩΒ±tΘΫ2s ±Θ§PQ”κΓ―Oœύ«–Θ°
ΓΨΫβΈωΓΩ
Β±PQ «‘≤ΒΡ«–œΏ ±Θ§άϊ”Ο«–œΏΒΡ–‘÷ Α―APΘ§PHΘ§CQΘ§BQΖ÷±π”Οt±μ ΨΘ§»ΜΚσάϊ”ΟΙ¥Ι…Ε®άμΨΆΩ…“‘«σ≥ωtΘ°
…ηPQ”κΓ―Oœύ«–”ΎΒψHΙΐΒψPΉςPEΓΆBCΘ§¥ΙΉψΈΣEΘ°
ΓΏ÷±Ϋ«Χί–ΈABCDΘ§ADΓΈBCΘ§ΓύPE=ABΘ°
ΓΏAP=BE=tΘ§CQ=2tΘ§ΓύBQ=BC©¹CQ=22©¹2tΘ§EQ=BQ©¹BE=22©¹2t©¹t=22©¹3tΘΜ
ΓΏABΈΣΓ―OΒΡ÷±ΨΕΘ§ΓœABC=ΓœDAB=90ΓψΘ§ΓύADΓΔBCΈΣΓ―OΒΡ«–œΏΘ§ΓύAP=PHΘ§HQ=BQΘ§ΓύPQ=PH+HQ=AP+BQ=t+22©¹2t=22©¹tΘΜ
‘ΎRtΓςPEQ÷–Θ§PE2+EQ2=PQ2Θ§Γύ122+Θ®22©¹3tΘ©2=Θ®22©¹tΘ©2Θ§Φ¥ΘΚ8t2©¹88t+144=0Θ§Γύt2©¹11t+18=0Θ§Θ®t©¹2Θ©Θ®t©¹9Θ©=0Θ§Γύt1=2Θ§t2=9ΘΜ
ΓΏP‘ΎAD±Ώ‘ΥΕ·ΒΡ ±ΦδΈΣ![]() ΟκΘ°
ΟκΘ°
ΓΏt=9ΘΨ8Θ§Γύt=9Θ®…α»ΞΘ©Θ§ΓύΒ±t=2Οκ ±Θ§PQ”κΓ―Oœύ«–Θ°

 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ