题目内容
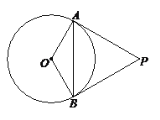
【题目】如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AB=![]() cm,将一块直角三角板的直角顶点放在点O处旋转,始终保持该直角三角板的两直角边分别与AC、BC相交,交点分别为D、E,则CD+CE=______cm.
cm,将一块直角三角板的直角顶点放在点O处旋转,始终保持该直角三角板的两直角边分别与AC、BC相交,交点分别为D、E,则CD+CE=______cm.
【答案】5
【解析】
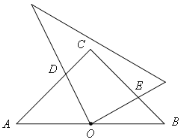
连接OC构建全等三角形,证明△ODC≌△OEB,得DC=BE;把CD+CE转化到同一条线段上,即求BC的长;通过等腰直角△ABC中斜边AB的长就可以求出BC=5,则CD+CE=BC=5.
解:连接OC,

∵等腰直角△ABC中,AB=5![]() ,
,
∴∠B=45°,
∴cos∠B=![]() ,
,
∴BC=5![]() ×cos45°=5
×cos45°=5![]() ×
×![]() =5,
=5,
∵点O是AB的中点,
∴OC=![]() AB=OB,OC⊥AB,
AB=OB,OC⊥AB,
∴∠COB=90°,
∵∠DOC+∠COE=90°,∠COE+∠EOB=90°,
∴∠DOC=∠EOB,
同理得∠ACO=∠B,
∴△ODC≌△OEB,
∴DC=BE,
∴CD+CE=BE+CE=BC=5.
故答案为:5.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
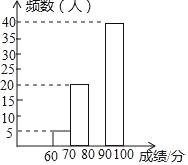
【题目】某校组织了一次全校2000名学生参加的比赛,赛后发现所有参赛学生的成绩均不低于60分,为了更好地了解本次大赛的成绩分布情况,随机抽取了100名学生的成绩(成绩x取整数,满分100分)作为样本进行整理,得到下列不完整的统计表:
请依据所给信息,解答下列问题:
(1)直接填空:a= ,b= ,c= ;
(2)请补全频数分布直方图;
(3)请自己提出一个与该题信息相关的问题,并解答你提出的问题.
成绩x/分 | 频数 | 频率 |
60≤x<70 | 5 | 0.05 |
70≤x<80 | 20 | b |
80≤x<90 | a | c |
90≤x≤100 | 40 | 0.40 |