题目内容
【题目】已知:在平面直角坐标系xOy中,二次函数![]()
![]() 的图像与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,△ABC的面积为12.
的图像与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,△ABC的面积为12.
(1)求这个二次函数的解析式;
(2)点D的坐标为![]() ,点P在二次函数的图像上,∠ADP为锐角,且
,点P在二次函数的图像上,∠ADP为锐角,且![]() ,请直接写出点P的横坐标;
,请直接写出点P的横坐标;
(3)点E在x轴的正半轴上,![]() ,点O与点
,点O与点![]() 关于EC所在直线对称,过点O作
关于EC所在直线对称,过点O作![]() 的垂线,垂足为点N,ON与EC交于点M.若
的垂线,垂足为点N,ON与EC交于点M.若![]() ,求点E的坐标.
,求点E的坐标.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)点E的坐标为
;(3)点E的坐标为![]()
【解析】
(1)根据对称轴坐标公式可求二次函数图象的对称轴,当![]() 时,
时,![]() ,可求点C的坐标为
,可求点C的坐标为![]() ,根据三角形面积公式可求
,根据三角形面积公式可求![]() ,进一步得到A点和B点的坐标分别为
,进一步得到A点和B点的坐标分别为![]() ,
,![]()
![]() ,再用待定系数法即可求二次函数的解析式;
,再用待定系数法即可求二次函数的解析式;
(2)作![]() 轴于点F.分两种情况:(ⅰ)当点P在直线AD的下方时;(ⅱ)当点P在直线AD的上方时,延长
轴于点F.分两种情况:(ⅰ)当点P在直线AD的下方时;(ⅱ)当点P在直线AD的上方时,延长![]() 至点G使得
至点G使得![]() ,连接DG,作
,连接DG,作![]() 轴于点H,两种情况讨论可求点
轴于点H,两种情况讨论可求点![]() 的坐标;
的坐标;
(3)连接![]() ,交CE于T.连接
,交CE于T.连接![]() ,根据三角函数的整数可得
,根据三角函数的整数可得![]() ,同理
,同理![]() ,得到
,得到![]() ,从而得到点E的坐标.
,从而得到点E的坐标.
(1)当x = 0时,![]() ,∴
,∴ ![]() ,
,
∵ ![]() ,∴ AB = 6,
,∴ AB = 6,
又∵ 二次函数图像的对称轴是直线![]() ,
,
∴ ![]() ,
,![]() ,
,
∴ ![]() ,解得
,解得![]() ,
,
∴ 二次函数的解析式为![]() ,
,
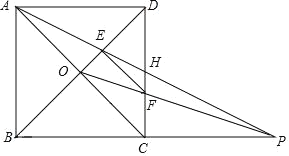
(2)如图,作![]() 轴于点F.分两种情况:
轴于点F.分两种情况:
(ⅰ)当点P在直线AD的下方时,如图所示,
由(1)得点![]() ,点
,点![]() ,
,
∴DF=1,AF=2,
在Rt△ADF中,,![]() ,得
,得![]() .
.
延长DF与抛物线交于点![]() ,则
,则![]() 点即为所求.
点即为所求.
将x=-2代入抛物线解析式,得y=-4,
∴点![]() 的坐标为
的坐标为![]() .
.
(ⅱ)当点P在直线AD的上方时,延长![]() 至点G使得
至点G使得![]() ,连接DG,作
,连接DG,作![]() 轴于点H,如图所示,在
轴于点H,如图所示,在![]() 与
与![]() 中,
中,
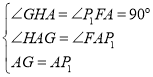
∴![]() ≌
≌![]() (AAS).
(AAS).
![]() ,
,![]()
又![]() ,
,![]()
∴点G的坐标是![]()
在![]() 中,
中, ![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
设DG与抛物线的交点为![]() ,则
,则![]() 点为所求.
点为所求.
作![]() 于点K,作
于点K,作![]() 交DK于点S.
交DK于点S.
设![]() 点的坐标为
点的坐标为![]() ,
,
则![]() ,
,
![]() .
.
由![]() ,
,![]() ,
,![]() ,得
,得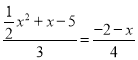 .
.
整理,得![]()
解得![]() .
.
![]() 点在第二象限,横坐标为负,
点在第二象限,横坐标为负,
![]() 点的横坐标为
点的横坐标为![]()
综上,P点的横坐标为![]() 或
或![]() .
.
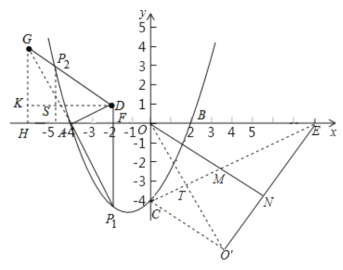
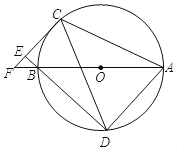
(3)如图,联结![]() ,交EC于点T,联结
,交EC于点T,联结![]() .
.
∵ 点O与点![]() 关于EC所在直线对称,
关于EC所在直线对称,
∴ ![]() ⊥EC,
⊥EC,![]() ,
,![]() .
.
∴ ![]() ⊥
⊥![]()
又∵ ON⊥![]() ,∴
,∴ ![]() ∥ON.
∥ON.
∴ ![]() .
.
∴ OC = OM
∴ CT = MT
在Rt△ETO中,∠ETO = 90°,![]() .
.
在Rt△COE中,∠COE = 90°,![]() .
.
∴ ![]()
∴ ![]()
同理可得![]()
∴ ![]()
∵ ![]() ,∴ OE = 8
,∴ OE = 8
∵ 点E在x轴的正半轴上
∴ 点E的坐标为![]() .
.