题目内容
已知一次函数 的图象过点(98,19),它与X轴的交点为(P,0),与y轴交点为(0,q),若p是质数,q是正整数,那么满足条件的所有一次函数的个数为( )。
的图象过点(98,19),它与X轴的交点为(P,0),与y轴交点为(0,q),若p是质数,q是正整数,那么满足条件的所有一次函数的个数为( )。
 的图象过点(98,19),它与X轴的交点为(P,0),与y轴交点为(0,q),若p是质数,q是正整数,那么满足条件的所有一次函数的个数为( )。
的图象过点(98,19),它与X轴的交点为(P,0),与y轴交点为(0,q),若p是质数,q是正整数,那么满足条件的所有一次函数的个数为( )。| A.0 | B.1 | C.2 | D.大于2的整数 |
A
把点(98,19)代入y=ax+b,得98a+b=19;把(p,0),(0,q)也代入y=ax+b,得b=q,a="-" 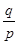 .所以19p=-98q+pq,则q=
.所以19p=-98q+pq,则q=  ,p是质数,q是正整数,再利用整除的性质讨论即可.
,p是质数,q是正整数,再利用整除的性质讨论即可.
解:把点(98,19)代入y=ax+b,得98a+b=19;
把(p,0),(0,q)也代入y=ax+b,得b=q,a=-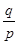 .
.
所以19p=-98q+pq,
则q= ,p是质数,q是正整数,分子只有三个因数即1、19、p,则p-98只能等于1、19或p,解的p都不是质数.
,p是质数,q是正整数,分子只有三个因数即1、19、p,则p-98只能等于1、19或p,解的p都不是质数.
所以满足条件的所有一次函数的个数为0.
故答案为A.
本题考查了一次函数的性质,点在图象上,则点的横纵坐标满足解析式.也考查了质数的概念和整数的整除性质.
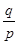 .所以19p=-98q+pq,则q=
.所以19p=-98q+pq,则q=  ,p是质数,q是正整数,再利用整除的性质讨论即可.
,p是质数,q是正整数,再利用整除的性质讨论即可.解:把点(98,19)代入y=ax+b,得98a+b=19;
把(p,0),(0,q)也代入y=ax+b,得b=q,a=-
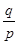 .
.所以19p=-98q+pq,
则q=
 ,p是质数,q是正整数,分子只有三个因数即1、19、p,则p-98只能等于1、19或p,解的p都不是质数.
,p是质数,q是正整数,分子只有三个因数即1、19、p,则p-98只能等于1、19或p,解的p都不是质数.所以满足条件的所有一次函数的个数为0.
故答案为A.
本题考查了一次函数的性质,点在图象上,则点的横纵坐标满足解析式.也考查了质数的概念和整数的整除性质.

练习册系列答案
相关题目
 千米/分钟,甲到达B地立即返回.乙所乘冲锋舟在在静水中的速度
千米/分钟,甲到达B地立即返回.乙所乘冲锋舟在在静水中的速度 为
为 千米/分钟.已知A、B两地的距离为20千米,水流速度为
千米/分钟.已知A、B两地的距离为20千米,水流速度为 千米/分钟,甲、乙乘冲锋舟行驶的距离y(千米)与所用时间x(分钟)之间的函数图象如图所示.
千米/分钟,甲、乙乘冲锋舟行驶的距离y(千米)与所用时间x(分钟)之间的函数图象如图所示.
 关系如下表:
关系如下表: 与
与 满足初中学过的某一函数关系,求函数的解析式;
满足初中学过的某一函数关系,求函数的解析式;

 的取值情况进行分析,说明按哪种优惠方法购买比较便宜;
的取值情况进行分析,说明按哪种优惠方法购买比较便宜; 中,AB=AC=2,
中,AB=AC=2, ,
, 是
是 边上一个动点,过点
边上一个动点,过点
 ,交
,交 .若设
.若设 ,
, 的面积为
的面积为 ,则
,则
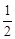
 的图象上,则点Q(a,3a﹣5)位于第_________象限
的图象上,则点Q(a,3a﹣5)位于第_________象限