Question

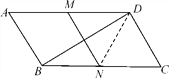
【题目】如图，在平行四边形ABCD中，按下列条件得到的四边形EFGH不一定是平行四边形的是( )

A.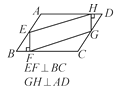

B.

C.

D.

Answer 1

【答案】A

【解析】选项A，由于所给已知条件只有角的关系，三角形边之间没有等量关系，不能证明三角形全等或边之间平行，也就无法证明四边形EFGH是平行四边形；选项B，连接AC，根据三角形中位线定理，易证EF=GH且EF∥GH，即可得四边形EFGH是平行四边形；选项C，利用AD∥BC，AE、BE是角平分线，易证∠ABE=90°，即可得∠HEF=90°，同理可得∠EFH=∠FGH=∠EHG=90°，从而易证四边形EFGH是矩形，继而得四边形EFGH是平行四边形； 选项D，设平行四边形ABCD对角线的交点为O，由于ABCD是平行四边形，那么∠EAO=∠GCO，且∠AOE=∠COG，OA=OC，利用ASA可证△AOE≌△COG，那么OE=OG，同理OH=OF，从而易证四边形EFGH是平行四边形．故选A．