题目内容
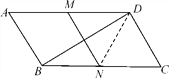
【题目】如图,在平行四边形ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD.
(1)求证:四边形MNCD是平行四边形;
(2)求证:BD=![]() MN.
MN.
【答案】见解析
【解析】试题分析:(1)要证明四边形MNCD是平行四边形,即要证明MD=NC,MD∥NC,由四边形ABCD是平行四边形可得AD=BC,AD∥BC,又因为M、N分别是AD、BC的中点,所以MD=NC,MD∥NC;(2)连结ND,由四边形MNCD是平行四边形可得 MN=DC,因为N是BC的中点,所以BN=CN,结合BC=2CD,∠C=60°可以得出△NCD是等边三角形,进而得出ND=NC,∠DNC=60°,由三角形外角的性质可得∠NBD+∠NDB=∠DNC,
因为DN=NC=NB,所以∠DBN=∠BDN=![]() ∠DNC=30°,所以∠BDC=90°,最后结合tan∠DBC可证明DB=
∠DNC=30°,所以∠BDC=90°,最后结合tan∠DBC可证明DB=![]() MN.
MN.
试题解析:
(1)∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,
∵M、N分别是AD、BC的中点,∴MD=NC,MD∥NC,
∴四边形MNCD是平行四边形;
(2)连结ND,
∵四边形MNCD是平行四边形,∴MN=DC,
∵N是BC的中点,∴BN=CN,
∵BC=2CD,∠C=60°,∴△NCD是等边三角形,∴ND=NC,∠DNC=60°,
∵∠DNC是△BND的外角,∴∠NBD+∠NDB=∠DNC,
∵DN=NC=NB,∴∠DBN=∠BDN=![]() ∠DNC=30°,∴∠BDC=90°,
∠DNC=30°,∴∠BDC=90°,
∵tan∠DBC=tan30°=![]() =
=![]() ,
,
∴DB=![]() DC=
DC=![]() MN.
MN.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目