题目内容
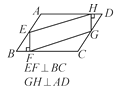
【题目】如图,在△ABC中,AB=AC,以AB为直径的半圆交BC于点D,过点D作EF⊥AC于点F,交AB的延长线于点E. 
(1)求证:EF是⊙O的切线;
(2)当BD=3,DF= ![]() 时,求直径AB.
时,求直径AB.
【答案】
(1)证明:连结OD.
∵EF⊥AC,
∴∠DFA=90°,
∵AB=AC,
∴∠1=∠C,
∵OB=OD,
∴∠1=∠2,
∴∠2=∠C,
∴OD∥AC,
∴∠EDO=∠DFA=90°,即OD⊥EF.
∴EF是⊙O的切线

(2)解:连结AD,
∵AB是直径
∴AD⊥BC,
又AB=AC,
∴CD=BD=3,
在Rt△CFD中,DF= ![]() ,
,
∴CF= ![]() =
= ![]() ,
,
在Rt△CFD中,DF⊥AC,
∴△CFD∽△DFA,
∴ ![]() =
= ![]() ,即AF=
,即AF= ![]() =
= ![]() ,
,
∴AC=CF+AF= ![]() +
+ ![]() =5,
=5,
∴AB=AC=5.

【解析】(1)连结OD.根据垂直的定义得到∠DFA=90°,根据等腰三角形的性质得到∠1=∠C,∠1=∠2,等量代换得到∠2=∠C,根据平行线的性质得到∠EDO=∠DFA=90°,即OD⊥EF.于是得到结论;(2)连结AD,根据勾股定理得到CF= ![]() =
= ![]() ,根据相似三角形的性质得到AF=
,根据相似三角形的性质得到AF= ![]() =
= ![]() ,于是得到结论.
,于是得到结论.
【考点精析】认真审题,首先需要了解等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角)).

练习册系列答案
相关题目