题目内容
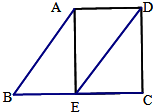 23、如图,已知AB∥DE,∠BAE=∠EDC,AD⊥AE,垂足为A,请在下划线内补全求∠ADC的度数的解题过程或依据.
23、如图,已知AB∥DE,∠BAE=∠EDC,AD⊥AE,垂足为A,请在下划线内补全求∠ADC的度数的解题过程或依据.解:∵AB∥DE (已知),
∴∠BAE=
∠AED
(两直线平行,内错角相等
).∵∠BAE=∠EDC(已知),
∴
∠AED=∠EDC
(等量代换).∴
AE∥CD
(内错角相等,两直线平行
).∴
∠AEC=∠ECD
(两直线平行,同旁内角互补).又∵AD⊥AE (已知),
∴∠EA D=
90°
(垂直的概念).∴∠ADC=
90°
(两直线平行,同旁内角互补
).分析:根据平行线的判定和性质,进行填空即可.
解答:解:∵AB∥DE (已知),
∴∠BAE=∠AED(两直线平行,内错角相等 ).
∵∠BAE=∠EDC(已知),
∴∠AED=∠EDC(等量代换).
∴AE∥CD(内错角相等,两直线平行 ).
∴(两直线平行,同旁内角互补).
又∵AD⊥AE (已知),
∴∠EA D=90° (垂直的概念).
∴∠ADC=90°( 两直线平行,同旁内角互补).
故答案为:∠AED,两直线平行,内错角相等,∠AED=∠EDC,AE∥CD,
内错角相等,两直线平行,∠AEC=∠ECD,90°,90°,两直线平行,同旁内角互补.
∴∠BAE=∠AED(两直线平行,内错角相等 ).
∵∠BAE=∠EDC(已知),
∴∠AED=∠EDC(等量代换).
∴AE∥CD(内错角相等,两直线平行 ).
∴(两直线平行,同旁内角互补).
又∵AD⊥AE (已知),
∴∠EA D=90° (垂直的概念).
∴∠ADC=90°( 两直线平行,同旁内角互补).
故答案为:∠AED,两直线平行,内错角相等,∠AED=∠EDC,AE∥CD,
内错角相等,两直线平行,∠AEC=∠ECD,90°,90°,两直线平行,同旁内角互补.
点评:本题考查了平行线的判定和性质,是基础知识要熟练掌握.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 5、如图,已知AB∥DE,∠A=136°,∠C=164°,则∠D的度数为( )
5、如图,已知AB∥DE,∠A=136°,∠C=164°,则∠D的度数为( ) 如图,已知AB=DE,BC=EF,∠B=∠E,A、F、C、D在同一条直线上,
如图,已知AB=DE,BC=EF,∠B=∠E,A、F、C、D在同一条直线上, 如图,已知AB∥DE,BC∥EF,D,C在AF上,且AD=CF,请补充完整过程,说明△ABC≌△DEF的理由.
如图,已知AB∥DE,BC∥EF,D,C在AF上,且AD=CF,请补充完整过程,说明△ABC≌△DEF的理由.
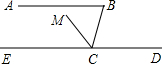 如图,已知AB∥DE,∠B=80°,CM平分∠BCE,求∠DCM的度数.
如图,已知AB∥DE,∠B=80°,CM平分∠BCE,求∠DCM的度数.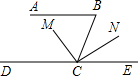 如图,已知AB∥DE,∠B=80°,CM平分∠BCD,CM⊥CN,垂足为C.求∠NCE的度数.
如图,已知AB∥DE,∠B=80°,CM平分∠BCD,CM⊥CN,垂足为C.求∠NCE的度数.