题目内容
 如图,已知AB=DE,BC=EF,∠B=∠E,A、F、C、D在同一条直线上,
如图,已知AB=DE,BC=EF,∠B=∠E,A、F、C、D在同一条直线上,(1)求证:EF∥BC;
(2)若AD=10,CF=4,求AF的长.
分析:(1)由于AB=DE,BC=EF,∠B=∠E,利用SAS可证△ABC≌△DEF,于是∠ACB=∠DFE,从而可得EF∥BC;
(2)由于△ABC≌△DEF,那么AC=DF,根据等式性质可证AF=CD,于是2AF+CF=10,易求AF.
(2)由于△ABC≌△DEF,那么AC=DF,根据等式性质可证AF=CD,于是2AF+CF=10,易求AF.
解答:证明:(1)在△ABC和△DEF中,
,
∴△ABC≌△DEF,
∴∠ACB=∠DFE,
∴EF∥BC;
(2)∵△ABC≌△DEF,
∴AC=DF,
∴AF+FC=CD+CF,
∴AF=CD,
∵AD=10,
∴2AF+CF=10,
∵CF=4,
∴AF=3.
|

∴△ABC≌△DEF,
∴∠ACB=∠DFE,
∴EF∥BC;
(2)∵△ABC≌△DEF,
∴AC=DF,
∴AF+FC=CD+CF,
∴AF=CD,
∵AD=10,
∴2AF+CF=10,
∵CF=4,
∴AF=3.
点评:本题考查了全等三角形的判定和性质,解题的关键是先证明△ABC≌△DEF.

练习册系列答案
相关题目
 5、如图,已知AB∥DE,∠A=136°,∠C=164°,则∠D的度数为( )
5、如图,已知AB∥DE,∠A=136°,∠C=164°,则∠D的度数为( ) 如图,已知AB∥DE,BC∥EF,D,C在AF上,且AD=CF,请补充完整过程,说明△ABC≌△DEF的理由.
如图,已知AB∥DE,BC∥EF,D,C在AF上,且AD=CF,请补充完整过程,说明△ABC≌△DEF的理由.
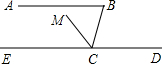 如图,已知AB∥DE,∠B=80°,CM平分∠BCE,求∠DCM的度数.
如图,已知AB∥DE,∠B=80°,CM平分∠BCE,求∠DCM的度数.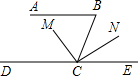 如图,已知AB∥DE,∠B=80°,CM平分∠BCD,CM⊥CN,垂足为C.求∠NCE的度数.
如图,已知AB∥DE,∠B=80°,CM平分∠BCD,CM⊥CN,垂足为C.求∠NCE的度数.