Question

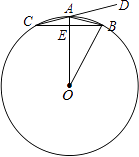
【题目】在Rt△ABC中，∠ACB=90°，∠A=30°，BD是△ABC的角平分线，DE⊥AB于点E.

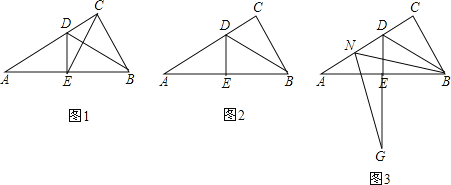
(1)如图1，连接EC，求证：△EBC是等边三角形；

(2)点M是线段CD上的一点(不与点C，D重合)，以BM为一边，在BM的下方作∠BMG=60°，MG交DE延长线于点G.求证：AD=DG+MD；

(3)点N是线段AD上的一点，以BN为一边，在BN的下方作∠BNG=60°，NG交DE延长线于点G.请在图3中画出图形，并直接写出ND，DG与AD数量之间的关系.

Answer 1

【答案】（1）证明见解析；（2）结论：AD=DG+DM，证明见解析；（3）结论：AD=DGDN.证明见解析.

【解析】

(1)、根据含有30°角的直角三角形的性质得出∠ABC=60°，BC=0.5AB，BE=0.5AB，从而得出等边三角形；(2)、延长ED使得DW=DM，连接MW，根据角平分线的性质以及直角三角形的性质得出△WDM是等边三角形，从而证明出△WGM和△DBM全等，得出答案；(3)、延长BD至H，使得DH=DN，利用直角三角形的性质证明出△DNG和△HNB全等，从而得出答案．

(1)证明：如图1所示：

在Rt△ABC中，∠ACB=90°，∠A=30°，∴∠ABC=60°，BC=0.5AB；

∵BD平分∠ABC，∴∠1=∠DBA=∠A=30°.∴DA=DB.

∵DE⊥AB于点E ∴AE=BE=0.5AB，∴BC=BE， ∴△EBC是等边三角形；

(2)结论：AD=DG+DM.

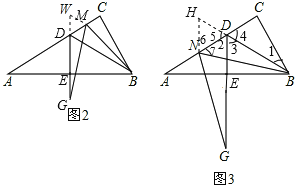
证明：如图2所示：延长ED使得DW=DM，连接MW，

∵∠ACB=90°，∠A=30°，BD是△ABC的角平分线，DE⊥AB于点E，

∴∠ADE=∠BDE=60°，AD=BD，又∵DM=DW， ∴△WDM是等边三角形，

∴MW=DM，∴△WGM≌△DBM，∴BD=WG=DG+DM，∴AD=DG+DM.

(3)结论：AD=DGDN．

证明：延长BD至H，使得DH=DN， 由(1)得DA=DB，∠A=30°.

∵DE⊥AB于点E， ∴∠2=∠3=60°，∴∠4=∠5=60°，∴△NDH是等边三角形

∴NH=ND ∠H=∠6=60°， ∴∠H=∠2， ∵∠BNG=60°，∴∠BNG+∠7=∠6+∠7.

即∠DNG=∠HNB， ∴△DNG≌△HNB(ASA)， ∴DG=HB.

∵HB=HD+DB=ND+AD， ∴DG=ND+AD， ∴AD=DGND．