��Ŀ����
����Ŀ���ӹ������������������ȹ������е�������ɡ�ȹ�����Ʒ����ʽ�����Ĺ�������ģʽ�ڸ�������Ѹ�ٵ��ռ������ݹ�����Ϣ���ķ������й��������÷�չ����2017��ʾ�����빲�����û��6 ���ˣ�����һ������Լ1���ˣ�
��1��Ϊ��ñ�����������빲�����û��Ϣ�����е��鷽ʽ�бȽϺ������ǣ� ����
A.��ijѧУ��ȫ��ͬѧ�����ʾ�����
B.��ijС����ס�������ʾ�����
C.��ȫ����IJ�ͬ���أ�ѡȡ������������ʾ�����
��2������С����������������������ﹲ�����������ij����������12��36�������1000�ˣ����������ȡ��100�ˣ�ͳ���������ﹲ�������������������������²�������ͳ��ͼ������ͼ��ʾ�� 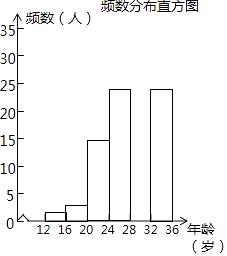
�ﹲ������������ͳ�Ʊ�
����Σ��꣩ | Ƶ�� | Ƶ�� |
12��x��16 | 2 | 0.02 |
16��x��20 | 3 | 0.03 |
20��x��24 | 15 | a |
24��x��28 | 25 | 0.25 |
28��x��32 | b | 0.30 |
32��x��36 | 25 | 0.25 |
����������Ϣ����������⣺
��ͳ�Ʊ��е�a=��b=��
�ڲ�ȫƵ���ֲ�ֱ��ͼ��
���Թ����������������20�굽32�꣨��20�꣬����32�꣩�ﹲ�������������ˣ�
���𰸡�
��1��C
��2��0.15��30�� 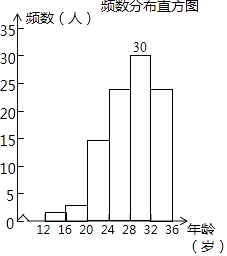 ��700
��700
���������⣺ ��2����a=15��100=0.15��b=100��0.3=30��
�۽⣺1000����0.15+0.25+0.3��=700���ˣ���
�𣺹����������������20�굽32�꣨��20�꣬����32�꣩�ﹲ������������700�ˣ�
���Դ��ǣ�0.15��30��700
�����㾫�����������⣬������Ҫ�˽�ȫ��������������(ȫ������ռ���������ȫ�桢ȷ����һ�㻨�Ѷࡢ��ʱ��������ijЩ���鲻����ȫ����飻����������л����١�ʡʱ���ص㣬����ȡ�������Ƿ���д����ԣ�ֱ�ӹ�ϵ����������Ƶ�ȷ�̶�)����Ҫ����Ƶ���ֲ�ֱ��ͼ(�ص㣺��������ʾ�����Ƶ���ֲ��������������ʾ�����Ƶ����𣮣�ע����������ͳ��ͼ��Ƶ���ֲ�ֱ��ͼ��)�����֪ʶ���Ǵ���Ĺؼ���

 Сѧ�̲���ȫ���ϵ�д�
Сѧ�̲���ȫ���ϵ�д�����Ŀ��Ϊ�˽�ij��������ɫ���С���ʽ�������ijУ��ѧ��ȤС�����ʾ��������ʽ�����������ij�в��ֳ����������Ҫ���з�ʽ�������ʾ����������ֻ���������������ѡ��һ�ࣩ���������������Ƴ����²�������ͳ��ͼ��
���� | A | B | C | D | E |
���з�ʽ | �������� | ���� | ������ | ��ʿ | ˽�ҳ� |
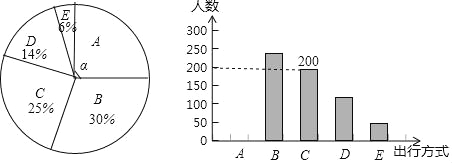
����������Ϣ���ش��������⣺
��1�����뱾���ʾ������������ �ˣ�����ѡ��B��������� �ˣ�
��2��������ͳ��ͼ�У���A���Ӧ����Բ�ĽǦ��Ķ���������ȫ����ͳ��ͼ��
��3������Լ��12���˳��У�����A��B��C��������з�ʽ����Ϊ����ɫ���С���ʽ������Ƹ��С���ɫ���С���ʽ��������