��Ŀ����
����Ŀ����֪���������ε����߳�������������������
��ϣ���ļ���ѧ�Һ������������⣬�����������������ۡ�һ���и����˼��㹫ʽ��������ʽS=![]() ������a��b��c�������ε����߳���p=
������a��b��c�������ε����߳���p=![]() ��SΪ�����ε����������������֤��
��SΪ�����ε����������������֤��
���磺�ڡ�ABC�У�a=3��b=4��c=5����ô������������������㣺
��a=3��b=4��c=5
��p=![]() =6
=6
��S=![]() =
=![]() =6
=6
��ʵ�ϣ�������֪�����ε����߳�����������������⣬�������ҹ�����ʱ����ѧ���ؾ���������ؾ��ع�ʽ�ȷ��������
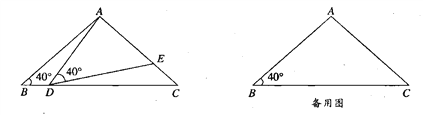
��ͼ���ڡ�ABC�У�BC=5��AC=6��AB=9
��1���ú���ʽ���ABC�������
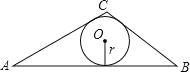
��2�����ABC������Բ�뾶r��
���𰸡���1��10![]() ����2��r=
����2��r=![]() ��
��
��������
�����������1���ȸ���BC��AC��AB�ij����P���ٴ��뵽��ʽS=![]() �������S��ֵ����2�����ݹ�ʽS=
�������S��ֵ����2�����ݹ�ʽS=![]() r��AC+BC+AB��������ɵù���r�ķ��̣��ⷽ�̵�r��ֵ��
r��AC+BC+AB��������ɵù���r�ķ��̣��ⷽ�̵�r��ֵ��
�����������1����BC=5��AC=6��AB=9��
��p=![]() =
=![]() =10��
=10��
��S=![]() =
=![]() =10
=10![]() ��
��
�ʡ�ABC�����10![]() ��
��
��2����S=![]() r��AC+BC+AB����
r��AC+BC+AB����
��10![]() =
=![]() r��5+6+9����
r��5+6+9����
��ã�r=![]() ��
��
�ʡ�ABC������Բ�뾶r=![]() ��
��

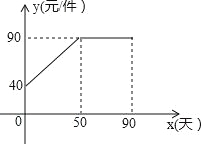
����Ŀ�����꼶��3������ѧ��ȤС�龭���г�����������ij����Ʒ�ڵ�x�죨1��x��90����xΪ���������ۼ����������������Ϣ���£���֪��Ʒ�Ľ���Ϊ30Ԫ/���������Ʒ���ۼ�Ϊy����λ��Ԫ/������ÿ���������Ϊp����λ��������ÿ�����������Ϊw����λ��Ԫ����
ʱ��x���죩 | 1 | 30 | 60 | 90 |
ÿ��������p������ | 198 | 140 | 80 | 20 |
��1�����w��x�ĺ�����ϵʽ��
��2�������۸���Ʒ�ڼ���ʱ����������������������������
��3������Ʒ�����۹����У����ж�����ÿ�������������5600Ԫ����ֱ��д�������