题目内容
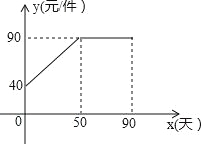
【题目】九年级（3）班数学兴趣小组经过市场调查整理出某种商品在第x天（1≤x≤90，且x为整数）的售价与销售量的相关信息如下．已知商品的进价为30元/件，设该商品的售价为y（单位：元/件），每天的销售量为p（单位：件），每天的销售利润为w（单位：元）．
时间x（天） | 1 | 30 | 60 | 90 |
每天销售量p（件） | 198 | 140 | 80 | 20 |
（1）求出w与x的函数关系式；
（2）问销售该商品第几天时，当天的销售利润最大？并求出最大利润；
（3）该商品在销售过程中，共有多少天每天的销售利润不低于5600元？请直接写出结果．
【答案】（1）w=
；（2）销售第45天时，当天获得的销售利润最大，最大利润是6050元；（3）该商品在销售过程中，共有24天每天的销售利润不低于5600元．
【解析】
试题分析：（1）当0≤x≤50时，设商品的售价y与时间x的函数关系式为y=kx+b，由点的坐标利用待定系数法即可求出此时y关于x的函数关系式，根据图形可得出当50＜x≤90时，y=90．再结合给定表格，设每天的销售量p与时间x的函数关系式为p=mx+n，套入数据利用待定系数法即可求出p关于x的函数关系式，根据销售利润=单件利润×销售数量即可得出w关于x的函数关系式；（2）根据w关于x的函数关系式，分段考虑其最值问题．当0≤x≤50时，结合二次函数的性质即可求出在此范围内w的最大值；当50＜x≤90时，根据一次函数的性质即可求出在此范围内w的最大值，两个最大值作比较即可得出结论；（3）令w≥5600，可得出关于x的一元二次不等式和一元一次不等式，解不等式即可得出x的取值范围，由此即可得出结论．
试题解析：（1）当0≤x≤50时，设商品的售价y与时间x的函数关系式为y=kx+b（k、b为常数且k≠0），
∵y=kx+b经过点（0，40）、（50，90），
∴
，解得：
，
∴售价y与时间x的函数关系式为y=x+40；
当50＜x≤90时，y=90．
∴售价y与时间x的函数关系式为y=
．
由书记可知每天的销售量p与时间x成一次函数关系，
设每天的销售量p与时间x的函数关系式为p=mx+n（m、n为常数，且m≠0），
∵p=mx+n过点（60，80）、（30，140），
∴
，解得：
，
∴p=﹣2x+200（0≤x≤90，且x为整数），
当0≤x≤50时，w=（y﹣30）p=（x+40﹣30）（﹣2x+200）=﹣2x2+180x+2000；
当50＜x≤90时，w=（90﹣30）（﹣2x+200）=﹣120x+12000．
综上所示，每天的销售利润w与时间x的函数关系式是w=．
（2）当0≤x≤50时，w=﹣2x2+180x+2000=﹣2（x﹣45）2+6050，
∵a=﹣2＜0且0≤x≤50，
∴当x=45时，w取最大值，最大值为6050元．
当50＜x≤90时，w=﹣120x+12000，
∵k=﹣120＜0，w随x增大而减小，
∴当x=50时，w取最大值，最大值为6000元．
∵6050＞6000，
∴当x=45时，w最大，最大值为6050元．
即销售第45天时，当天获得的销售利润最大，最大利润是6050元．
（3）当0≤x≤50时，令w=﹣2x2+180x+2000≥5600，即﹣2x2+180x﹣3600≥0，
解得：30≤x≤50，
50﹣30+1=21（天）；
当50＜x≤90时，令w=﹣120x+12000≥5600，即﹣120x+6400≥0，
解得：50＜x≤53
，
∵x为整数，
∴50＜x≤53，
53﹣50=3（天）．
综上可知：21+3=24（天），
故该商品在销售过程中，共有24天每天的销售利润不低于5600元．
