题目内容
平行四边形ABCD中,AC,BD是两条对角线,下列说法错误的是( )A.若∠ABC=90°,则四边形ABCD为矩形
B.若AC⊥BD,则四边形ABCD为矩形
C.若AB=BC,则四边形ABCD为菱形
D.若AC⊥BD且AC=BD则四边形ABCD为正方形
【答案】分析:A从矩形定义出发从而判断是正确的; B这种情况的除了正方形,它是矩形;还有菱形,它不是矩形,故不正确;C种情况,有正方形即为菱形,和菱形,故正确;D从从正方形的判定即可判断,即正确.
解答:解:A中若∠ABC=90°的平行四边形,通过平行线间的两角互补即为90°,可得证,故正确;
B若AC⊥BD,这种情况的除了正方形,它是矩形;还有菱形,它不是矩形,故不正确;
C若AB=BC的平行四边形,有正方形即为菱形,和菱形,故正确;
D若AC⊥BD的平行四边形为菱形,且AC=BD的即为正方形,故正确.
故选B.
点评:本题考查了正方形的判定,从其定义,以及正方形与菱形,矩形的区别.
解答:解:A中若∠ABC=90°的平行四边形,通过平行线间的两角互补即为90°,可得证,故正确;
B若AC⊥BD,这种情况的除了正方形,它是矩形;还有菱形,它不是矩形,故不正确;
C若AB=BC的平行四边形,有正方形即为菱形,和菱形,故正确;
D若AC⊥BD的平行四边形为菱形,且AC=BD的即为正方形,故正确.
故选B.
点评:本题考查了正方形的判定,从其定义,以及正方形与菱形,矩形的区别.

练习册系列答案
相关题目
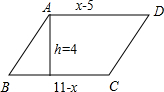 如图,在平行四边形ABCD中,高h=4,则平行四边形ABCD的面积S=
如图,在平行四边形ABCD中,高h=4,则平行四边形ABCD的面积S=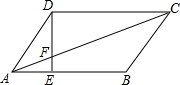 如图,在平行四边形ABCD中,AE:EB=1:2,S△AEF=3,则S△FCD=
如图,在平行四边形ABCD中,AE:EB=1:2,S△AEF=3,则S△FCD=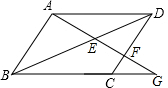 如图,在平行四边形ABCD中,E是BD上一点,AE的延长线交DC于点F,交BC的延长线于点G.求证:
如图,在平行四边形ABCD中,E是BD上一点,AE的延长线交DC于点F,交BC的延长线于点G.求证: 如图,在平行四边形ABCD中,E、F分别是AD、BC的中点,AC分别交BE、DF于G、H,下列结论:
如图,在平行四边形ABCD中,E、F分别是AD、BC的中点,AC分别交BE、DF于G、H,下列结论: 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.