Question

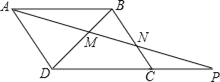
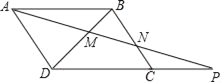
【题目】如图，已知四边形ABCD是平行四边形，P为DC延长线上一点，AP分别交BD，BC于点M，N．

(1)图中相似三角形共有_____对；

(2)证明：AM2＝MNMP；

(3)若AD＝6，DC：CP＝2：1，求BN的长．

Answer 1

【答案】(1)6；(2)证明见解析；(3)BN＝4．

【解析】

（1）根据相似三角形的判定定理来做：△ADB∽△CBD、△ABN∽△PCN、△ADM∽△NBM、△AMB∽△PMD、△APD∽△ABN；
（2）由四边形ABCD是平行四边形的性质来证明△ADM∽△NBM、△PDM∽△ABM；再由相似三角形的对应边成比例的性质知：＝、＝，所以AM2=MNMP．
（3）由四边形ABCD是平行四边形的性质来证明△PCN∽△PDA；再由相似三角形的对应边成比例的性质知：＝；最后根据已知条件求解即可．

(1)解：6；

有△AMB∽△PMD，△ADM∽△NBM，△ABN∽△PCN∽△PDA，△ABD≌△CDB，

∴共6对；

(2)证明：∵AD∥BC，

∴∠ADM＝∠NBM，∠DAM＝∠BNM，

∴△ADM∽△NBM，

∴＝；

∵AB∥DC，

∴∠P＝∠BAM，∠MDP＝∠ABM，

∴△PDM∽△ABM，

∴＝，

∴＝，

∴AM2＝MNMP；

(3)解：∵AD∥BC，

∴∠PCN＝∠PDA，∠P＝∠P，

∴△PCN∽△PDA，

∴＝，

∵DC：CP＝2：1，

∴＝＝；

又∵AD＝6

∴NC＝2，BN＝4