题目内容
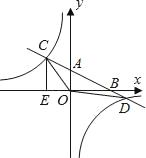
【题目】如图,∠AOD=∠COB=90°,∠COE=25°,EO是∠BOD的角平分线;
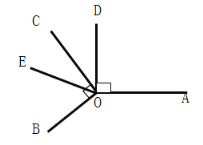
(1)找出图中除直角外的两对相等的角:
(2)求∠COD的度数,按要求填空:
因为∠COB=90°,∠COE=25°,
所以∠BOE=∠ -∠ =90°- °= °.
因为EO是∠BOD的角平分线,
所以∠ =∠BOE= °
所以∠COD=∠ -∠ = °- °= °.
【答案】(1)∠DOE=∠BOE,∠AOC=∠BOD;(2)COB,COE,25,65,DOE,65,DOE,COE,65,25,40.
【解析】
(1)由角平分线可得一对相等的角,再用两个直角分别加上∠COD可得一对相等的角;
(2)先求∠BOE,再根据角平分线得到∠DOE=∠BOE,再用∠DOE减去∠COE即可得到∠COD.
解:(1)∵EO是∠BOD的角平分线,
∴∠DOE=∠BOE
∵∠AOD=∠COB=90°
∴∠AOD+∠COD=∠COB+∠COD
即∠AOC=∠BOD
故填:∠DOE=∠BOE,∠AOC=∠BOD.
(2)因为∠COB=90°,∠COE=25°,
所以∠BOE=∠COB-∠COE=90°-25°=65°,
因为EO是∠BOD的角平分线,
所以∠DOE=∠BOE=65° ,
所以∠COD=∠DOE-∠COE=65°-25°=40°.
故填:COB,COE,25,65,DOE,65,DOE,COE,65,25,40.

练习册系列答案
相关题目
【题目】沾益区兴隆水果店计划用1000元购进甲、乙两种新出产的水果140千克,这两种水果的进价、售价如下表所示:
进价(元/千克) | 售价(元/千克) | |
甲 | 5 | 8 |
乙 | 9 | 13 |
(1)这两种水果各购进多少千克?
(2)该水果店全部销售完这批水果时获利多少元?