题目内容
【题目】某厂按用户的月需求量x(件)完成一种产品的生产,其中x>0.每件的售价为18万元,每件的成本y(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量x(件)成反比.经市场调研发现,月需求量x与月份n(n为整数,1≤n≤12)符合关系式x=2n2﹣2kn+9(k+3)(k为常数),且得到了表中的数据
月份n(月)1 | 1 | 2 |
成本y(万元/件) | 11 | 12 |
需求量x(件/月) | 120 | 100 |
(1)直接写出k的值;
(2)求y与x满足的关系式,请说明一件产品的利润能否是12万元;
(3)推断是否存在某个月既无盈利也不亏损.
【答案】(1)k=13;(2)一件产品的利润不可能是12万元;(3)不存在某个月既无盈利也不亏损.
【解析】试题分析:(1)根据已知月份与x的值,取一组需求量x与月份n代入x=2n2﹣2kn+9(k+3)即可求出k;
(2)根据题意得y=a+![]() ,由表中数据列方程组求解,即可得到y与x的关系式;
,由表中数据列方程组求解,即可得到y与x的关系式;
(3)根据不亏损也不盈利列方程求出x的值,进行解答;
解:(1)将n=1,x=120代入x=2n2-2kn+9(k+3),
得2×12-2k+9(k+3)=120,
解得k=13,
(2)设基础价为a,则根据题意可得y=a+![]() ,根据表格可得
,根据表格可得
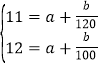 ,
,
解得![]() ,
,
∴y=6+![]() .
.
利润为12万元时,成本价为6万元,则![]() =0,
=0,
∵![]() >0,则一件产品的利润不能是12万元;
>0,则一件产品的利润不能是12万元;
(3)当n=2,x=100时也满足
当不盈利也不亏损时,成本价为18万元,
则6+600x=18,
解得x=50,
则50=2n2-26n+144,
即n2-13n+47=0.
方程根的判别式△=(-13)2-4×1×47<0,故方程无实根,
则不存在某个月既无盈利也不亏损.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案【题目】某天上午出租车司机小张在东西走向的大街上营运,如果规定向东为正,向西为负,他这天上午所接送六位乘客的行驶里程(单位:km)如下表:(等待乘客时,空车里程忽略不计)
乘客顺序 | 第一位 | 第二位 | 第三位 | 第四位 | 第五位 | 第六位 |
行驶里程 | -2 | +8 | -1 | +1 | -9 | -2 |
(1)将最后一位乘客送到目的地时,小张在出发地什么位置?
(2)若汽车耗油量为0.06![]() ,这天上午小张接送乘客,出租车共耗油多少升?
,这天上午小张接送乘客,出租车共耗油多少升?
(3)若出租车起步价为5元,起步里程为3km(包括3km),超过部分1.2元/km,问小张这天上午共收车费多少元?
【题目】沾益区兴隆水果店计划用1000元购进甲、乙两种新出产的水果140千克,这两种水果的进价、售价如下表所示:
进价(元/千克) | 售价(元/千克) | |
甲 | 5 | 8 |
乙 | 9 | 13 |
(1)这两种水果各购进多少千克?
(2)该水果店全部销售完这批水果时获利多少元?