题目内容
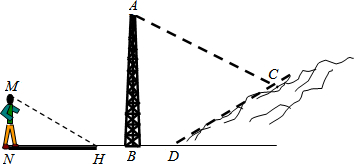
如图,在夕阳西下的傍晚,某人看见高压电线的铁塔在阳光的照射下,铁塔的影子的一部分落在小山的斜坡上,为了测得铁塔的高度,他测得铁塔底部B到小山坡脚D的距离为2米,铁塔在小山斜坡上的影长DC为3.4米,斜坡的坡度i=1:1.875,同时他测得自己的影长NH﹦336cm,而他的身长MN为168cm,求铁塔的高度.

考点:解直角三角形的应用-坡度坡角问题,相似三角形的应用
专题:
分析:作AC的延长线交BD的延长线于E,作CF⊥DE,垂足为F.利用勾股定理和相似三角形的性质求出DF,FE,从而得到BE的长,再用相似三角形的性质求出AB即可.
解答:解:作AC的延长线交BD的延长线于E,作CF⊥DE,垂足为F.

在Rt△CFD中,
i=1:1.875,
即CF:DF=1:1.875=8:15;
设CF=8x米,则DF=15x米,
由勾股定理可得,
(8x)2+(15x)2=CD2,
∴CD=17x=3.4,
∴x=0.2,
∴DF=15×0.2=3米,CF=8×0.2=1.6米.
∵FE:CF=NH:NM,
∴FE:1.6=336:168,
∴FE=3.2,
∴BE=BD+DF+FE=2+3+3.2=8.2米.
∴AB:BE=MN:NH,
∴AB:8.2=168:336,
∴AB=4.1米.
答:铁塔高度为4.1米.

在Rt△CFD中,
i=1:1.875,
即CF:DF=1:1.875=8:15;
设CF=8x米,则DF=15x米,
由勾股定理可得,
(8x)2+(15x)2=CD2,
∴CD=17x=3.4,
∴x=0.2,
∴DF=15×0.2=3米,CF=8×0.2=1.6米.
∵FE:CF=NH:NM,
∴FE:1.6=336:168,
∴FE=3.2,
∴BE=BD+DF+FE=2+3+3.2=8.2米.
∴AB:BE=MN:NH,
∴AB:8.2=168:336,
∴AB=4.1米.
答:铁塔高度为4.1米.
点评:本题考查了坡度与坡角及相似三角形的应用,构造直角三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目