Question

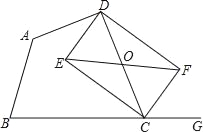
【题目】如图，点是菱形对角线的交点，，，连接交于点．

（1）求证：；

（2）若菱形的边长为2，且，求四边形的面积．

Answer 1

【答案】（1）证明见解析；（2）

【解析】

（1）通过证明四边形OCEB是矩形来推知OE=CB，根据是菱形，对角线垂直平分，已知，，可得四边形OCEB是平行四边形，由此即可推得四边形OCEB是矩形．

（2）已知四边形ABCD是菱形，，根据菱形的性质即可求得OC和OD的长，即可求出四边形的面积．

（1）∵四边形ABCD是菱形，

∴AC⊥BD

∵CE∥BD，EB∥AC，
∴四边形OCEB是平行四边形，
∴四边形OCEB是矩形，
∴OE=CB；

（2）∵四边形ABCD是菱形

∴OA=OC，OD=OB，∠CDO=∠ODA=∠CDA=30°

∴在Rt△COD中，OC=CD=1

∴

∵四边形OCEB是矩形

∴S四边形OCEB=OC×OB=1×=

故答案为：