题目内容
【题目】如图, 在![]() .
.
(1)用尺规作图方法,按要求作图:
①作![]() 的高
的高![]() ;
;
②作![]() 的平分线
的平分线![]() ,分别交
,分别交![]() 于点
于点![]() ;
;
(要求:保留作图痕迹,不写作法和证明)
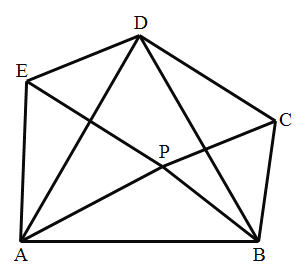
(2)求证:点![]() 在
在![]() 的垂直平分线.上; .
的垂直平分线.上; .
(3)在(1)所作的图中,探究线段AE与BF的数量关系,并证明你的结论.

【答案】(1)①见解析;②见解析;(2)证明见解析;(3)AE=2BF,证明见解析.
【解析】
(1)根据过已知直线外一点垂线的步骤作图;
(2)根据作角平分线的步骤作图;
(3)根据到线段两端点距离相等的点在线段的垂直平分线上,证明DA=DB即可;
(4)通过证△ADE≌△BDC得出AE=BC,再根据等腰三角形三线合一的性质得出BC=2BF即可得出结论.
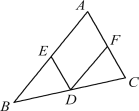
(1)①如图1,以B为圆心,BC为半径画弧,交AC于M;以C、M分别为圆心,以大于![]() 为半径画弧,两弧交于点P;作射线BP交AC于D,线段BD就是要求作的△ABC的高;
为半径画弧,两弧交于点P;作射线BP交AC于D,线段BD就是要求作的△ABC的高;
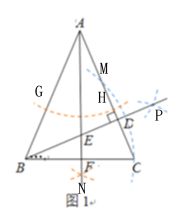
② 如图1,以A为圆心,以任意长为半径画弧,交AB,AC于G,H;以G,H分别为圆心,以大于![]() 为半径画弧,两弧交于N点;作射线AN,交BC于F点,射线AF就是所要求作的∠BAC的平分线;
为半径画弧,两弧交于N点;作射线AN,交BC于F点,射线AF就是所要求作的∠BAC的平分线;
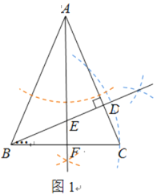
(2)∵∠BAC=45°,∠ADB=90°,
∴ ∠ABD=∠BAC=45°.
∴ DA=DB,
∴ 点D在AB的垂直平分线上.
 …
…
(3)∵ AB=AC,AF是∠BAC的角平分线,
∴ BC=2BF,AF⊥BC.
∴ ∠DAF+∠C=90°.
∵ ∠DBC+∠C=90°,
∴ ∠DAE=∠DBC.
又 ∵ DA=DB,∠ADE=∠BDC=90°,
∴ △ADE≌△BDC (ASA).
∴ AE=BC,
∴ AE=2BF.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目