题目内容
【题目】小孟同学将等腰直角三角板ABC(AC=BC)的直角顶点C放在一直线m上,将三角板绕C点旋转,分别过A,B两点向这条直线作垂线AD,BE,垂足为D,E.
(1)如图1,当点A,B都在直线m上方时,猜想AD,BE,DE的数量关系是 ;
(2)将三角板ABC绕C点按逆时针方向旋转至图2的位置时,点A在直线m上方,点B在直线m下方.(1)中的结论成立吗?请你写出AD,BE,DE的数量关系,并证明你的结论.
(3)将三角板ABC继续绕C点逆时针旋转,当点A在直线m的下方,点B在直线m的上方时,请你画出示意图,按题意标好字母,直接写出AD,BE,DE的数量关系结论 .

【答案】(1)DE=BE+AD;(2)DE=AD﹣BE,证明详见解析;(3)DE=AD+BE或DE=|AD﹣BE|.
【解析】
(1)先判断出∠CAD=∠BCE,进而得出△ACD≌△CBE,即可得出AD=CE,CD=BE,最后利用线段的和即可得出结论;
(2)先判断出∠CAD=∠BCE,进而得出△ACD≌△CBE,即可得出AD=CE,CD=BE,最后利用线段的差即可得出结论;
(3)先判断出∠CAD=∠BCE,进而得出△ACD≌△CBE,即可得出AD=CE,CD=BE,最后利用线段的和差即可得出结论.
解:(1)∵△ABC是等腰直角三角形,
∴AC=BC,∠ACD+∠BCE=90°,
∵AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠CAD=90°,
∴∠CAD=∠BCE,
∴△ACD≌△CBE,
∴CD=BE,AD=CE,
∴DE=CD+CE=BE+AD;
故答案为:DE=BE+AD;
(2)∵△ABC是等腰直角三角形,
∴AC=BC,∠ACD+∠BCE=90°,
∵AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠CAD=90°,
∴∠CAD=∠BCE,
∴△ACD≌△CBE,
∴CD=BE,AD=CE,
∴![]()
(3)如图3,
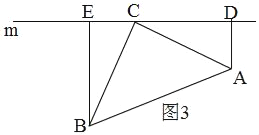
当点A,B在直线m同侧时,同(1)的方法得,△ACD≌△BCE,
∴CD=BE,AD=CE,
∴DE=CE+CD=AD+BE,
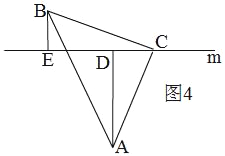
Ⅰ、当点A,B在直线m异侧时,如图4,同(2)的方法得,△ACD≌△BCE,
∴CD=BE,AD=CE,
∴![]()
Ⅱ、如图5,
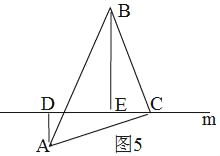
同Ⅰ的方法得,![]()
故答案为:DE=AD+BE或![]()

 天天向上口算本系列答案
天天向上口算本系列答案




