题目内容
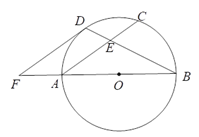
【题目】如图,AB是⊙O的直径,C是⊙O上一点,D是![]() 的中点,BD交AC于点E,过点D作DF∥AC交BA的延长线于点F.
的中点,BD交AC于点E,过点D作DF∥AC交BA的延长线于点F.
(1)求证:DF是⊙O的切线;
(2)若AF=2,FD=4,求tan∠BEC的值.
【答案】(1)证明见解析;(2)tan∠BEC=2
【解析】分析:(1)欲证明DF是⊙O的切线,只要证明OD⊥DF ,OD⊥AC
即可。(2)连接AD,在△ODF中利用勾股定理可求出⊙O的半径,由△ABE∽△FBD可得AE=3,再由△BDA∽△ADE可得![]() ,而∠BEC=∠AED从而即可得出结果。
,而∠BEC=∠AED从而即可得出结果。
本题解析:
(1)证明:连接OD
∵D是![]() 的中点 ∴OD⊥AC
的中点 ∴OD⊥AC
∵DF∥AC ∴OD⊥DF
∵OD为⊙O的半径 ∴直线AB是⊙O的切线
(2)连接AD,设⊙O的半径为r,则OD=OA=r,OF=2+r
∵∠ODF=90°, ∴![]() ,解得:r=3,∴AB=6,BF=8
,解得:r=3,∴AB=6,BF=8
∵DF∥AC,∴△ABE∽△FBD, ∴![]() ,即
,即![]() ,∴AE=3
,∴AE=3
∵D是![]() 的中点,∴∠B=∠DAE ,
的中点,∴∠B=∠DAE ,
∵∠BDA=∠ADE,∴△BDA∽△ADE, ∴![]() ,
,
AB是⊙O的直径, ∴∠ADB=90°, ∴tan∠AED=![]()
∵∠BEC=∠AED,∴tan∠BEC=2

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目