Question

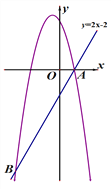
【题目】已知直线y=2x-2与抛物线交于点A（1，0）和点B，且m＜n．

（1）当m=时，直接写出该抛物线顶点的坐标.

（2）求点B的坐标（用含m的代数式表示）.

（3）设抛物线顶点为C，记△ABC的面积为S.

①，求线段AB长度的取值范围；

②当时，求对应的抛物线的函数表达式

Answer 1

【答案】（1）（﹣，）；（2）B点坐标为（﹣2，﹣6）；（3）①5≤AB≤9；②或

【解析】试题分析：

（1）把点A（1，0）代入中可得n=-2m，结合m=-2可得二次函数的解析式，再配方即可求得其图象的顶点坐标了；

（2）联立一次函数和二次函数的解析式组成方程组，解方程组即可求得点B的坐标；

（3）①由（2）中所得点B的坐标结合点A的坐标可用含m的代数式表达出AB2=，由可得，这样即可得到AB2在的范围内随着m的增大而减小，将m=-3和m=-1分别代入AB2的表达式即可求得AB2的最大值和最小值，由此即可求得对应的AB的最大值和最小值了，从而可得AB的取值范围；

②设抛物线的对称轴与直线AB交于点E，由已知条件易得点E的坐标为，用含m的代数式表达出抛物线的顶点的坐标，这样即可由S=S△CEB+S△ACD=，结合已知条件用列出关于m的方程，解方程即可求得对应的m的值，将所得m的值代入抛物线的解析式中即可求得对应的解析式.

试题解析：

（1）∵抛物线y=mx2+mx+n过点A（1，0），得n=﹣2m，

∴抛物线的解析式为：，

又∵m==-2，

∴抛物线的解析式为，

∴抛物线的顶点坐标为（﹣，）；

（2）由 消去y可得：mx2+（m﹣2）x﹣2m+2=0，

即x2+（1﹣）x﹣2+=0， 解得x=1或x=﹣2，

∴B点坐标为（﹣2，﹣6），

（3）①由勾股定理可得AB2=，

∵，

∴ ，

∴AB2随的增大而减小，

∴当=-3时，AB2有最大值405，则AB有最大值，

当=-1时，AB2有最小值125，则AB有最小值，

∴线段AB长度的取值范围为≤AB≤；

②如下图，设抛物线对称轴交直线AB于点E，

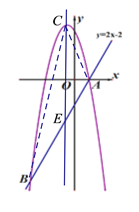
∵抛物线对称轴为x=﹣，点E在直线AB：y=2x﹣2上，

∴E（﹣，﹣3），

∵A（1，0），B，且m＜0，设△ABC的面积为S，

∴S=S△CEB+S△ACD=(+3）（3-）=，解得m=-1或m=，

对应的抛物线的函数表达式为或.