��Ŀ����
����Ŀ���ס���������ĩ��ͬһ�ص����ȥij���㣬������ʱ���£����������ȳ������׳���0.2Сʱ���ҿ�����ǰ���������ʻ��ʱ��Ϊx��h�����ס���������ʻ��·�̷ֱ�Ϊy1��km����y2��km������ͼ����y1��y2����x�ĺ���ͼ�� 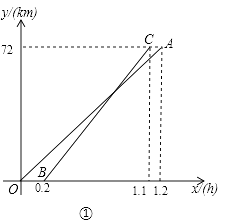
��1���ֱ����߶�OA���߶�BC����ʾ��y1��y2����x�ĺ�������ʽ��
��2����xΪ����ʱ���������6km��
��3�����������Sǧ�ף���ͼ��������ֱ������ϵ�л���S����x�ĺ���ͼ�� 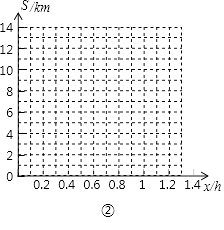
���𰸡�
��1���⣺��OA��y1=k1x��BC��y2=k2x+b��
��y1=k1x���㣨1.2��72����
����y1=60x��
��y2=k2x+b���㣨0.2��0������1.1��72����
�� ![]() ��
��
��� ![]() ��
��
��y2=80x��16��
��2���⣺��60x=6��
���x=0.1��
��60x����80x��16��=6��
���x=0.5��
��80x��16��60x=6��
���x=1.1��
�ʵ�xΪ0.1��0.5��1.1Сʱ���������6ǧ�ף�
��3���⣺��ͼ��ʾ��
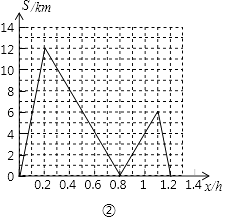
����������1�����ݴ���ϵ���������߶�OA���߶�BC����ʾ��y1��y2����x�ĺ�������ʽ����2����3���������0��x��0.2���ڼס�����������ǰ���ۼס������������������ۿ���x��ֵ����3����4���������0��x��0.2���ڼס�����������ǰ���ۼס��������������ҵ��ᄚ��ǰ���ܼס��������������ҵ��ᄚ��������ۿɻ���S����x�ĺ���ͼ��

����Ŀ��С����С����Ͷ���ӣ��ʵؾ��ȵ������壩��ʵ������Ϸ��
��1����ʵ�������ǹ�����50�����飬���������£�
���ϵĵ��� | 1 | 2 | 3 | 4 | 5 | 6 |
���ֵĴ��� | 10 | 9 | 6 | 9 | 8 | 8 |
����գ��˴�ʵ���У���1�㳯�ϡ���Ƶ���� ��
��2������Ϸʱ����Լ����ÿ��ͬʱ����ö���ӣ������ö���ӵĵ���֮�ͳ���6����С����ʤ������С����ʤ����С����С��˭��ʤ�Ŀ����Դ���˵�����ɣ�