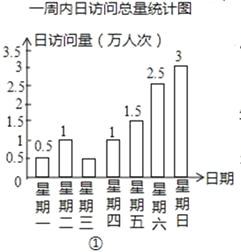
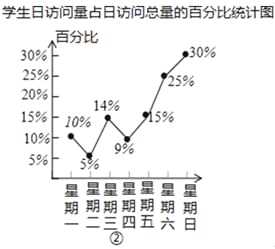
题目内容
【题目】如图，2条直线 最多有
＝1个交点，3条直线最多有
＝3个交点，4条直线最多有
＝6个交点，……由此猜想，8条直线最多有＿＿＿个交点.
A. 32 B. 16 C. 28 D. 40
【答案】C
【解析】
由已知中两条相交直线最多有1个交点，三条直线最多有3个交点，四条直线最多有6个交点点，五条直线最多有10个交点，我们分析n值变化过程中，交点最多个数的变化趋势，找出规律后，归纳为一般性公式即可得到答案．
令n条直线最多交点个数为M：
两条相交直线最多有1个交点，即n=2，M=1，
三条直线最多有3个交点，即n=3，M=3，
四条直线最多有6个交点点，即n=4，M=6，
五条直线最多有10个交点，即n=5，M=10，
…
则n条直线最多交点个数M=1+2+3+4+…+（n-1）=
，
当n=8时，
=28，
故选：C．
练习册系列答案
相关题目
