题目内容
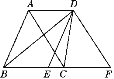
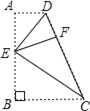
【题目】如图,四边形ABCD中,AD∥BC,∠B=90°,E为AB上一点,分别以ED,EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边上的点F处,若AD=2,BC=6,则EF的值是( )
A. 2![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2![]()
【答案】A
【解析】
如图,首先运用翻折变换的性质求出CF、DF的长度,证明∠DEC=90°;进一步证明△EFD∽△CFE,由相似三角形对应边成比例即可求出EF的长度.
如图,由翻折变换的性质得:
CF=CB=6,DF=DA=2,∠EFC=∠B=90°;
∠AED=∠FED,∠BEC=∠FEC,∴∠DEC![]() 180°=90°∵∠EDC+∠DCE=90°,∠EDC+∠DEF=90°,∴∠DEF=∠DCE,∵∠EFD=∠CFE=90°,∴△EFD∽△CFE,∴EF:CF=DF:EF,∴EF2=DFFC=2×6=12,∴EF=2
180°=90°∵∠EDC+∠DCE=90°,∠EDC+∠DEF=90°,∴∠DEF=∠DCE,∵∠EFD=∠CFE=90°,∴△EFD∽△CFE,∴EF:CF=DF:EF,∴EF2=DFFC=2×6=12,∴EF=2![]() .
.
故选A.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
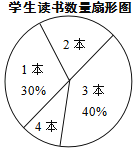
【题目】某校七年级共有500名学生,在“世界读书日”前夕,开展了“阅读助我成长”的读书活动.为了解该年级学生在此次活动中课外阅读情况,童威随机抽取m名学生,调查他们课外阅读书籍的数量,将收集的数据整理成如下统计表和扇形图.
学生读书数量统计表
阅读量/本 | 学生人数 |
1 | 15 |
2 | a |
3 | b |
4 | 5 |
(1)直接写出m、a、b的值;
(2)估计该年级全体学生在这次活动中课外阅读书籍的总量大约是多少本?