Question

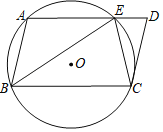
【题目】如图，在ABCD中，过A、B、C三点的⊙O交AD于点E，连接BE、CE，BE＝BC．

（1）求证：△BEC∽△CED；

（2）若BC＝10，DE＝3.6，求⊙O的半径．

Answer 1

【答案】(1)见解析； （2）

【解析】

（1）证明两个等腰三角形相似，证明一个底角对应相等即可；

（2）利用直径构造直角三角形，从而涉及到半径（直径），再利用垂径定理即可解决问题．

（1）证明：∵BE＝BC，

∴∠BEC＝∠BCE

∵四边形ABCD是平行四边形，

∴AD∥BC，AB∥CD．

∴∠BCE＝∠DEC，∠A+∠D＝180°．

∴∠BEC＝∠DEC

∵四边形ABCD内接于⊙O，

∴∠A+∠BCE＝180°．

∴∠BCE＝∠D

∴△BEC∽△CED

即得证．

（2）过点O作OF⊥CE，垂足为F，连接OC，如下图．

∴CF＝CE，

∴直线OF垂直平分CE，

∵BE＝BC，

∴直线OF经过点B，

∵△BEC∽△CED，又由（1）可知CE＝CD，

∴，

∵BC＝10，DE＝3.6，

∴CE＝CD＝6

∴CF＝CE＝3，

设⊙O的半径为r，

可得BF＝，OF＝﹣r，

在Rt△OCF中，OF2+CF2＝OC2，

∴（﹣r）2+9＝r2

∴r＝，

即圆的半径为．