��Ŀ����
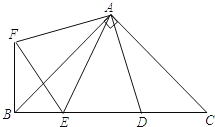
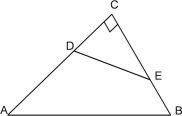
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬AC=16cm��AB=20cm������D�ɵ�C���A��ÿ��1 cm�ٶ��ڱ�AC���˶�������E�ɵ�C���B��ÿ��![]() cm�ٶ��ڱ�BC���˶�������D����E�ӵ�Cͬʱ�������˶�t��(t>0)������DE.
cm�ٶ��ڱ�BC���˶�������D����E�ӵ�Cͬʱ�������˶�t��(t>0)������DE.
��1����֤����DCE�ס�BCA��
��2���辭����D��C��E�����ԲΪ��P.
�ٵ���P���AB����ʱ����t��ֵ.
���ڵ�D����E�˶������У�����P���AB���ڵ�F��G����F�ڵ�G��ࣩ������CP ���ӳ�CP����AB�ڵ�M������PFM���CDE����ʱ����t��ֵ.

���𰸡���1������������2����![]() ���ڵ�
���ڵ�![]() ��
��![]() ����ʱ��
����ʱ��![]() ��
��![]() .
.
��������
��1��������ã�![]() ����
����![]() ��
��![]() ��
��![]() ���ù��ɶ������
���ù��ɶ������![]() ����
����![]() ���ó�
���ó�![]() ����
����![]() ����
����![]() ��
��![]() ��
��
��2��������![]() ���ӳ�
���ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]() ������ֱ�������ε�б�����ߵó�
������ֱ�������ε�б�����ߵó�![]() Ϊ
Ϊ![]() �е㣬
�е㣬![]() ���ó�
���ó�![]() ������
������![]() ��
��![]() ���ó�
���ó�![]() , �����ýǵĵ����滻�ó�
, �����ýǵĵ����滻�ó�![]() ����
����![]() ���ʡ�P���
���ʡ�P���![]() ���У��������Ǻ������DE,CE�������t�����������
���У��������Ǻ������DE,CE�������t�����������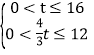 ���
���![]() ,�ɢٵ�
,�ɢٵ�![]() ,
,![]() ��
��![]() ����
����![]() ,
,![]() ��
��![]() ,�ٸ������������η�������ۼ������.
,�ٸ������������η�������ۼ������.
��1��֤����������ã�![]() ����
����![]() ��
��![]() ��
��![]() ��
��
��![]() ����
����![]() ��
��
��![]()
�֡�![]()
��![]() ��
��![]() ��
��
��2��������![]() ���ӳ�
���ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��

��![]() ��
��
��DE�ǡ�![]() ��ֱ��
��ֱ��
��![]() Ϊ
Ϊ![]() �е㣬
�е㣬
��![]() .
.
��![]() ����
����![]() ��
��![]() ����
����![]() ,
,
��![]() ,��
,��![]()
��![]() ��
��
�ߡ�P���![]() ���У�
����
���![]() Ϊ�е㣬
Ϊ�е㣬 ![]() Ϊ��
Ϊ��![]() ��ֱ����
��ֱ����
��![]() ���
���![]() ����
����![]()
![]() ��
��![]() ��
��![]() .
.
���������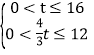 ���
���![]() ,�ɢٵ�
,�ɢٵ�![]() ,
,![]() ��
��![]()
��,
![]() ��
��![]() ,
,
��![]()
����![]() ��
��![]() ���ƿɵã�
���ƿɵã�
���һ��![]() ��
��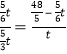 ��ã�
��ã�![]() �� 0��
�� 0��![]() ��9
��9
�������![]() ��
��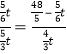 ��ã�
��ã�![]() �� 0��
�� 0��![]() ��9
��9
��������������![]() ��
��![]() ����ʱ.
����ʱ. ![]() ��
��![]()

 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�