题目内容
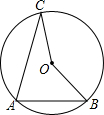
如图,⊙O的半径为1,弦AB=
,AC=
,则∠BOC=______.
| 2 |
| 3 |

作OD⊥AB于D,OE⊥AC于E,连结OA,OA=1,如图,
∴AD=BD=
AB=
,AE=CE=
AC=
,
在Rt△OAE中,OE=
=
,
∴∠EAO=30°,
在Rt△OAD中,OD=
=
,
∴∠DAO=45°,
∴∠BAC=45°+30°=75°,
∴∠BOC=2∠BAC=150°.
故答案为150°.

∴AD=BD=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
在Rt△OAE中,OE=
| OA2-AE2 |
| 1 |
| 2 |
∴∠EAO=30°,
在Rt△OAD中,OD=
| OA2-AD2 |
| ||
| 2 |
∴∠DAO=45°,
∴∠BAC=45°+30°=75°,
∴∠BOC=2∠BAC=150°.
故答案为150°.


练习册系列答案
相关题目