题目内容
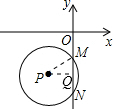
如图，半径为5的⊙P与y轴交于点M（0，-4），N（0，-10），函数y=
(x＜0)的图象过点P，求k的值．
| k |
| x |
过P作PQ⊥y轴，与y轴交于Q点，连接PM，
∴Q为MN的中点，
∵M（0，-4），N（0，-10），
∴OM=4，ON=10，
∴MN=10-4=6，
∴MQ=NQ=3，OQ=OM+MQ=4+3=7，
在Rt△PMQ中，PM=5，MQ=3，
根据勾股定理得：PQ=
=4，
∴P（-4，-7），
将x=-4，y=-7代入反比例函数y=
中得：-7=
，
则k=28．
∴Q为MN的中点，
∵M（0，-4），N（0，-10），
∴OM=4，ON=10，
∴MN=10-4=6，
∴MQ=NQ=3，OQ=OM+MQ=4+3=7，
在Rt△PMQ中，PM=5，MQ=3，
根据勾股定理得：PQ=
| PM2-MQ2 |
∴P（-4，-7），
将x=-4，y=-7代入反比例函数y=
| k |
| x |
| k |
| -4 |
则k=28．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
