题目内容
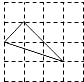
【题目】学完“证明(二)”一章后,老师布置了一道思考题:如图,点M、N分别在正三角形ABC的边BC.CA上,且BM=CN,AM、BN交于点Q。求证:∠BQM=60°。
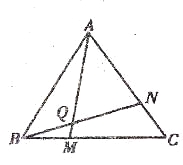
(1)请你完成这道思考题;
(2)做完(1)后,同学们在老师的启发下进行了反思,提出了许多问题,如:
①若将题中“BM=CN”与“∠BQM=60°”的位置交换,得到的是否仍是真命题?
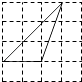
②若将题中的点M,N分别移动到BC,CA的延长线上,是否仍能得到∠BQM=60°?
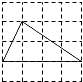
③若将题中的条件“点M,N分别在正三角形ABC的BC、CA边上”改为“点M,N分别在正方形ABCD的BC,CD边上”,是否仍能得到∠BQM=60°?对②,③进行证明。(自己画出对应的图形)
【答案】(1)见解析;(2)①是;②是;③否
【解析】
试题(1)根据正三角形的性质可得AB=BC,∠ABM=∠BCN,再结合BM=CN根据“SAS”可证得△ABM![]() △BCN,可得∠BAM=∠CBN,即可求得结果;
△BCN,可得∠BAM=∠CBN,即可求得结果;
(2)①仍为真命题;②易证△BAN![]() △ACM(SAS),可得∠1=∠2,∠N=∠M,即可求得结果;
△ACM(SAS),可得∠1=∠2,∠N=∠M,即可求得结果;
③易证△ABM![]() △BCN(SAS),可得∠1=∠2,又∠2+∠3=90°,即得∠BQM=∠1+∠3=∠2+∠3=90°.
△BCN(SAS),可得∠1=∠2,又∠2+∠3=90°,即得∠BQM=∠1+∠3=∠2+∠3=90°.
(1)∵正三角形ABC
∴AB=BC,∠ABM=∠BCN
∵BM=CN
∴△ABM![]() △BCN(SAS)
△BCN(SAS)
∴∠BAM=∠CBN,
∴∠BQM=∠BAQ+∠ABQ=∠MBQ+∠ABQ=60°;
(2)①仍为真命题;
②如图:
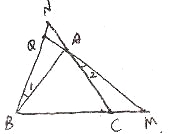
易证△BAN![]() △ACM(SAS)
△ACM(SAS)
∴∠1=∠2,∠N=∠M
又∠BQM=∠N+∠QAN=∠N+∠2=∠M+∠2=∠ACB=60°;
③如图
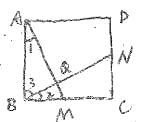
此时不能得到∠BQM=60°,而有∠BQM=90°
易证△ABM![]() △BCN(SAS)
△BCN(SAS)
∴∠1=∠2,又∠2+∠3=90°,
∴∠BQM=∠1+∠3=∠2+∠3=90°.