题目内容
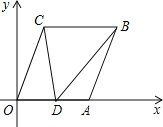
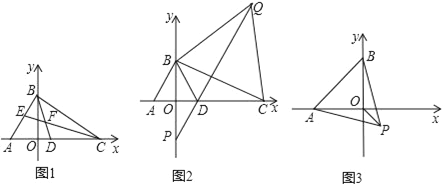
【题目】如图,在平面直角坐标系中,A(﹣3,0),点 B是 y轴正半轴上一动点,点C、D在 x正半轴上.
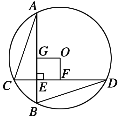
(1)如图,若∠BAO=60°,∠BCO=40°,BD、CE 是△ABC的两条角平分线,且BD、CE交于点F,直接写出CF的长_____.
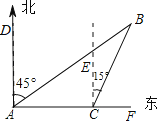
(2)如图,△ABD是等边三角形,以线段BC为边在第一象限内作等边△BCQ,连接 QD并延长,交 y轴于点 P,当点 C运动到什么位置时,满足 PD=![]() DC?请求出点C的坐标;
DC?请求出点C的坐标;
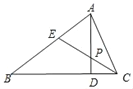
(3)如图,以AB为边在AB的下方作等边△ABP,点B在 y轴上运动时,求OP的最小值.
【答案】(1)6;(2)C的坐标为(12,0);(3)![]() .
.
【解析】
(1)作∠DCH=10°,CH 交 BD 的延长线于 H,分别证明△OBD≌△HCD 和△AOB≌△FHC,根据全等三角形的对应边相等解答;
(2)证明△CBA≌△QBD,根据全等三角形的性质得到∠BDQ=∠BAC=60°,求出 CD,得到答案;
(3)以 OA 为对称轴作等边△ADE,连接 EP,并延长 EP 交 x 轴于点 F.证明点 P 在直线 EF 上运动,根据垂线段最短解答.
解:(1)作∠DCH=10°,CH 交 BD 的延长线于 H,
∵∠BAO=60°,
∴∠ABO=30°,
∴AB=2OA=6,
∵∠BAO=60°,∠BCO=40°,
∴∠ABC=180°﹣60°﹣40°=80°,
∵BD 是△ABC 的角平分线,
∴∠ABD=∠CBD=40°,
∴∠CBD=∠DCB,∠OBD=40°﹣30°=10°,
∴DB=DC,
在△OBD 和△HCD 中,
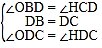
∴△OBD≌△HCD(ASA),
∴OB=HC,
在△AOB 和△FHC 中,
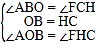
∴△AOB≌△FHC(ASA),
∴CF=AB=6,
故答案为6;
(2)∵△ABD 和△BCQ 是等边三角形,
∴∠ABD=∠CBQ=60°,
∴∠ABC=∠DBQ,
在△CBA 和△QBD 中,
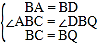
∴△CBA≌△QBD(SAS),
∴∠BDQ=∠BAC=60°,
∴∠PDO=60°,
∴PD=2DO=6,
∵PD=![]() DC,
DC,
∴DC=9,即 OC=OD+CD=12,
∴点 C的坐标为(12,0);
(3)如图3,以 OA为对称轴作等边△ADE,连接 EP,并延长 EP交 x 轴于点F.
由(2)得,△AEP≌△ADB,
∴∠AEP=∠ADB=120°,
∴∠OEF=60°,
∴OF=OA=3,
∴点P在直线 EF上运动,当 OP⊥EF时,OP最小,
∴OP=![]() OF=
OF=![]()
则OP的最小值为![]() .
.

 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案