题目内容
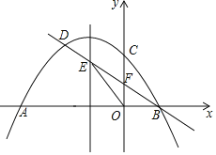
【题目】如图,四边形![]() 是以原点
是以原点![]() 为对称中心的矩形,
为对称中心的矩形,![]() ,
,![]() ,
,![]() 和
和![]() 分别与
分别与![]() 轴交于点
轴交于点![]() 、
、![]() ,连接
,连接![]() .
.

(1)写出点![]() 和点
和点![]() 的坐标;
的坐标;
(2)求四边形![]() 的面积;
的面积;
(3)判断点![]() 在矩形
在矩形![]() 的内部还是外部;
的内部还是外部;
(4)要使直线![]() 与矩形
与矩形![]() 没有公共点,直接写出
没有公共点,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;(2)5;(3)点
;(2)5;(3)点![]() 在矩形的内部;(4)
在矩形的内部;(4) ![]() 或
或![]()
【解析】
解:(1)∵四边形ABCD是以原点O为对称中心的矩形,
∴点A和点C、点B和点D关于原点对称,
∵![]() ,
,![]()
∴![]() ,
,![]() ;
;
(2)设直线CD的解析式为![]() ,
,
将点C、D的坐标分别代入![]() 得
得![]() ,
,
解得![]() ,
,
∴直线CD的解析式为![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
如解图,过点O作![]() 、
、![]() ,垂足分别为点M、N,
,垂足分别为点M、N,
∵四边形ABCD为矩形,
∴![]() ,
,![]() ,
,
如解图,连接OC,
∴![]() ;
;
(3)在直线CD的解析式![]() 上,当
上,当![]() 时,
时,![]() ,
,
∵![]() ,
,
∴点![]() 在点
在点![]() 的上方,
的上方,
又∵![]() ,
,
∴点![]() 在矩形的内部;
在矩形的内部;
(4) ![]() 或
或![]() .
.
【解法提示】当直线![]() 过A或C点时,直线与矩形只有一个公共点,
过A或C点时,直线与矩形只有一个公共点,
把![]() 代入
代入![]() ,得
,得![]() ,解得
,解得![]() ,
,
把![]() 代入
代入![]() ,得
,得![]() ,解得
,解得![]() ,
,
∴当直线![]() 与矩形ABCD没有公共点时,m的取值范围为
与矩形ABCD没有公共点时,m的取值范围为![]() 或
或![]() .
.

【题目】假期里,小红和小惠去买菜,三次购买的西红柿价格和数量如下表:
单价/(元/千克) | 4 | 3 | 2 | 合计 |
小红购买的数量/千克 | 1 | 2 | 3 | 6 |
小惠购买的数量/千克 | 2 | 2 | 2 | 6 |
(1)小红和小惠购买西红柿数量的中位数、众数是多少?
(2)从平均价格看,谁买的西红柿要便宜些.请思考下面小亮和小明的说法,你认为谁说得对?为什么?
小亮的说法
每次购买单价相同,购买总量也相同,平均价格应该也一样,都是![]() (元/千克),所以两人购买的西红柿一样便宜.
(元/千克),所以两人购买的西红柿一样便宜.
小明的说法
购买的总量虽然相同,但小红花了16元,小惠花了18元,平均价格不一样,所以小红购买的西红柿便宜.
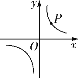
(3)小明在直角坐标系中画出反比例函数的图象,图象经过点![]() (如图),点
(如图),点![]() 的横、纵坐标分别为小红和小惠购买西红柿价格的平均数.
的横、纵坐标分别为小红和小惠购买西红柿价格的平均数.
①求此反比例函数的关系式;
②判断点![]() 是否在此函数图象上.
是否在此函数图象上.