题目内容
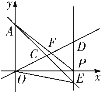
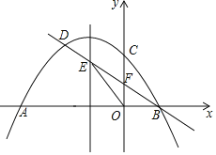
【题目】如图,抛物线![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,过点B的直线与抛物线的另一个交点为D,与抛物线的对称轴交于点E,与y轴交于点F,且
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,过点B的直线与抛物线的另一个交点为D,与抛物线的对称轴交于点E,与y轴交于点F,且![]() ,△OBE的面积为
,△OBE的面积为![]() .
.
(1)求抛物线的解析式;
(2)设P为已知抛物线上的任意一点,当△ACP的面积等于△ACB的面积时,求点P的坐标;
(3)点Q(0,m)是y轴上的动点,连接AQ、BQ,当∠AQB为钝角时,则m的取值范围是 .(直接写出答案)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 且
且![]()
【解析】
(1)首先根据抛物线解析式找到抛物线的对称轴,然后根据平行线分线段成比例得出HG=HO=1,OB=2,进而求出点B的坐标,然后根据△OBE的面积及平行线分线段成比例得出点D的坐标,最后利用待定系数法即可求解;
(2)首先根据抛物线的解析式求出A,C的坐标,然后利用待定系数法求出直线AC的解析式,然后设![]() ,则
,则![]() ,利用
,利用![]() ACP的面积等于
ACP的面积等于![]() ACB的面积建立一个关于m的方程,解方程求解即可;
ACB的面积建立一个关于m的方程,解方程求解即可;
(3)先利用勾股定理求出当![]() 时m的值,以及排除当A,Q,B三点共线时的m的值,即可得出当∠AQB为钝角时m的取值范围.
时m的值,以及排除当A,Q,B三点共线时的m的值,即可得出当∠AQB为钝角时m的取值范围.
解:(1)作DG⊥x轴于G,对称轴交x轴于H,如图,

∵抛物线为![]() ,
,
∴对称轴为直线x=﹣![]() =﹣1,则OH=1.
=﹣1,则OH=1.
![]()
∴OF∥EH∥DG,
∴GH:HO:OB=DE:EF:FB=1:1:2,
∴HG=HO=1,OB=2,
∴B(2,0).
∵△OBE的面积为![]() ,
,
∴![]() ×2×EH=
×2×EH=![]() ,解得EH=
,解得EH=![]() .
.
∵OF∥EH∥DG,
∴![]() =
=![]() =
=![]() ,则DG=
,则DG=![]() ×
×![]() =3,
=3,
∴D(﹣2,3).
把B(2,0),D(﹣2,3)代入y=ax2+2ax+c中,得
![]() 解得
解得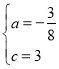
∴抛物线解析式为y=﹣![]() x2﹣
x2﹣![]() x+3 ;
x+3 ;
(2)令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,解得
,解得![]() .
.
![]() ,
,
![]() .
.
设直线AC的解析式为![]() ,
,
将![]() 代入解析式中得
代入解析式中得
![]() 解得
解得![]()
∴直线AC的解析式为y=![]() x+3.
x+3.
过点P作PQ⊥x轴交AC于点Q,

设![]() ,则
,则![]() ,
,
![]() ,
,
即![]() ,
,
当![]() 时,
时,
解得![]() ,
,
当![]() 时,
时,
![]()
此时![]() 与
与![]() 重合,故舍去;
重合,故舍去;
当![]() 时,
时,
![]()
此时![]() .
.
当![]() 时,
时,
化简得![]() ,
,
此时![]() ,
,
∴该方程无实数根,
综上所述,点P的坐标为![]() ;
;
(3)由(2)知,![]() ,
,
又∵![]() ,
,
![]() .
.
当![]() 时,
时,
![]() ,
,
即![]() ,
,
解得![]() .
.
当![]() 时,A,B,Q三点共线,不符合题意,
时,A,B,Q三点共线,不符合题意,
∴![]() ,
,
∴∠AQB为钝角时,则m的取值范围是![]() 且
且![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案【题目】如表是一个4×4(4行4列共16个“数”组成)的奇妙方阵,从这个方阵中选四个“数”,而且这四个“数”中的任何两个不在同一行,也不在同一列,有很多选法,把每次选出的四个“数”相加,其和是定值,则方阵中第三行三列的“数”是( )
30 |
| 2 | 22 |
﹣3 | ﹣2 | ﹣ | 0 |
|﹣5| | 6 | 23 | |
( | 4 |
| ( |
A. 5 B. 6 C. 7 D. 8