МвДҝДЪИЭ
ЎҫМвДҝЎҝЈЁ1Ј©ОКМв·ўПЦ
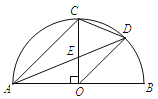
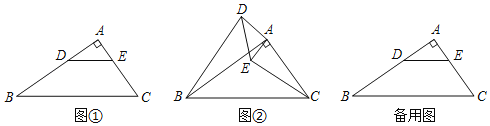
ИзНјўЩЈ¬ФЪRtЎчABCЦРЈ¬ЎПAЈҪ90ЎгЈ¬ABЈҪkACЈ¬өгDКЗABЙПТ»өгЈ¬DEЎОBCЈ®
МоҝХЈәBDЈ¬CEөДКэБҝ№ШПөОӘЎЎ ЎЎЈ»О»ЦГ№ШПөОӘЎЎ ЎЎЈ»
ЈЁ2Ј©АаұИМҪҫҝ
ИзНјўЪЈ¬Ҫ«ЎчADEИЖЧЕөгAЛіКұХлРэЧӘЈ¬РэЧӘҪЗОӘҰБЈЁ0ЎгЈјҰБЎЬ90ЎгЈ©Ј¬Б¬ҪУBDЈ¬CEЈ¬ЗлОКЈЁ1Ј©ЦРөДҪбВЫ»№іЙБўВрЈҝИфіЙБўЈ¬ЗлёшіцЦӨГчЈ¬ИфІ»іЙБўЈ¬ЗлЛөГчАнУЙЈ®
ЈЁ3Ј©НШХ№СУЙм
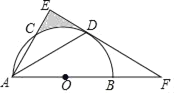
ФЪЈЁ2Ј©өДМхјюПВЈ¬Ҫ«ЎчADEИЖөгAЛіКұХлРэЧӘЈ¬РэЧӘҪЗОӘҰБЈ¬ЦұПЯBDЈ¬CEҪ»УЪөгFЈ¬ИфACЈҪ1Ј¬ABЈҪ![]() Ј¬өұЎПACEЈҪ15ЎгКұЈ¬ЗлЦұҪУРҙіцBFөДіӨЈ®
Ј¬өұЎПACEЈҪ15ЎгКұЈ¬ЗлЦұҪУРҙіцBFөДіӨЈ®
Ўҫҙр°ёЎҝЈЁ1Ј©ОКМв·ўПЦЈәBDЈҪkCEЈ»BDЎНCEЈ»ЈЁ2Ј©АаұИМҪҫҝЈәЈЁ1Ј©ЦРөДҪбВЫ»№іЙБўЈ¬АнУЙјыҪвОцЈ»ЈЁ3Ј©НШХ№СУЙмЈәBFөДіӨОӘ![]() »т
»т![]() Ј®
Ј®
ЎҫҪвОцЎҝ
ЈЁ1Ј©УЙЖҪРРПЯ·ЦПЯ¶ОіЙұИАэҝЙөГ![]() Ј¬УЙТСЦӘМхјюјҙҝЙөГBD=kECЈ»УЙЎПA=90ЎгјҙҝЙөГіцBDЎНCEЈ»
Ј¬УЙТСЦӘМхјюјҙҝЙөГBD=kECЈ»УЙЎПA=90ЎгјҙҝЙөГіцBDЎНCEЈ»
ЈЁ2Ј©НЁ№эЦӨГчЎчABDЎЧЎчACEЈ¬ҝЙөГ![]() =kЈ¬јҙҝЙөГBD=kECЈ»ФЩЦӨіцЎПBFC=90ЎгЈ¬јҙҝЙөГіцBDЎНCEЈ»
=kЈ¬јҙҝЙөГBD=kECЈ»ФЩЦӨіцЎПBFC=90ЎгЈ¬јҙҝЙөГіцBDЎНCEЈ»
ЈЁ3Ј©·ЦБҪЦЦЗйҝцМЦВЫЈ¬УЙПаЛЖИэҪЗРОөДРФЦКҝЙөГЎПACE=ЎПABDЈ¬јҙҝЙЦӨЎПBFC=90ЎгЈ¬УЙЦұҪЗИэҪЗРОөДРФЦКәН№ҙ№Й¶ЁАнҝЙЗуBFөДЦөЈ®
ЈЁ1Ј©ОКМв·ўПЦЈә
ҪвЈәЎЯDEЎОBCЈ¬
Ўа![]() ЈҪ
ЈҪ![]() Ј¬
Ј¬
ЎЯABЈҪkACЈ¬
ЎаBDЈҪkCEЈ¬
ЎЯЎПAЈҪ90ЎгЈ¬
ЎаABЎНACЈ¬
ЎаBDЎНCEЈ»
№Кҙр°ёОӘЈәBDЈҪkCEЈ»BDЎНCEЈ»
ЈЁ2Ј©АаұИМҪҫҝЈә
ҪвЈәЈЁ1Ј©ЦРөДҪбВЫ»№іЙБўЈ¬АнУЙИзПВЈә
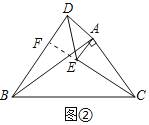
СУіӨCEҪ»BDУЪFЈ¬ИзНјўЪЛщКҫЈә
УЙРэЧӘөДРФЦКҝЙЦӘЈ¬ЎПBADЈҪЎПCAEЈ¬
ЎЯDEЎОBCЈ¬
Ўа![]() ЈҪ
ЈҪ![]() Ј¬
Ј¬
Ўа![]() ЈҪ
ЈҪ![]() Ј¬
Ј¬
ЎаЎчABDЎЧЎчACEЈ¬
Ўа![]() ЈҪ
ЈҪ![]() ЈҪkЈ¬ЎПABDЈҪЎПACEЈ¬
ЈҪkЈ¬ЎПABDЈҪЎПACEЈ¬
ЎаBDЈҪkECЈ»
ЎЯЎПCBF+ЎПBCFЈҪЎПABD+ЎПABC+ЎПBCFЈҪЎПACE+ЎПBCF+ЎПABCЈҪЎПACB+ЎПABCЈҪ90ЎгЈ¬
ЎаЎПBFCЈҪ90ЎгЈ¬
ЎаBDЎНCEЈ»
ЈЁ3Ј©НШХ№СУЙмЈә
ҪвЈәУЙРэЧӘөДРФЦКҝЙЦӘЈәЎПBADЈҪЎПCAE
ЎЯ![]() ЈҪ
ЈҪ![]() Ј¬
Ј¬
ЎаЎчABDЎЧЎчACEЈ¬
ЎаЎПACEЈҪ15ЎгЈҪЎПABDЈ¬
ЎЯЎПABC+ЎПACBЈҪ90ЎгЈ¬
ЎаЎПFBC+ЎПFCBЈҪ90ЎгЈ¬
ЎаЎПBFCЈҪ90ЎгЈ¬
ЎЯЎПBACЈҪ90ЎгЈ¬![]() Ј¬
Ј¬
ЎаtanЎПABCЈҪ![]() Ј¬
Ј¬
ЎаЎПABCЈҪ30ЎгЈ¬
ЎаЎПACBЈҪ60ЎгЈ¬
·ЦБҪЦЦЗйҝцЈә
ўЩ0ЎгЈјҰБЎЬ90ЎгКұЈ¬ИзНјўЪЛщКҫЈә
ЎаФЪRtЎчBACЦРЈ¬ЎПABCЈҪ30ЎгЈ¬ACЈҪ1Ј¬
ЎаBCЈҪ2ACЈҪ2Ј¬
ЎЯФЪRtЎчBFCЦРЈ¬ЎПCBFЈҪ30Ўг+15ЎгЈҪ45ЎгЈ¬BCЈҪ2Ј¬
ЎаBFЈҪCFЈҪ![]() Ј»
Ј»
ўЪҰБЈҫ90ЎгКұЈ¬ИзНјўЫЛщКҫЈә
ЙиCFЈҪaЈ¬ФЪBFЙПИЎөгGЈ¬К№ЎПBCGЈҪ15Ўг
ЎЯЎПBCFЈҪ60Ўг+15ЎгЈҪ75ЎгЈ¬ЎПCBFЈҪЎПABC©ҒЎПABDЈҪ30Ўг©Ғ15ЎгЈҪ15ЎгЈ¬
ЎаЎПCFBЈҪ90ЎгЈ¬
ЎаЎПGCFЈҪ60ЎгЈ¬ЎПCBFЈҪЎПBCGЈ¬
ЎаCGЈҪBGЈҪ2aЈ¬GFЈҪ![]() aЈ®
aЈ®
ЎаBFЈҪBG+GFЈҪЈЁ2+![]() Ј©aЈ¬
Ј©aЈ¬
ЎЯCF2+BF2ЈҪBC2
Ўаa2+ЈЁ2a+![]() aЈ© 2ЈҪ22Ј¬
aЈ© 2ЈҪ22Ј¬
ҪвөГЈәa2ЈҪ2©Ғ![]() Ј¬
Ј¬
ЎаaЈҪ![]() Ј¬
Ј¬
ЎаBFЈҪЈЁ2+![]() Ј©
Ј©![]() ЈҪ
ЈҪ![]() ЈҪ
ЈҪ![]() ЈҪ
ЈҪ![]() Ј»
Ј»
јҙЈәBFөДіӨОӘ![]() »т
»т![]() Ј®
Ј®

 УҰУГМвЧчТөұҫПөБРҙр°ё
УҰУГМвЧчТөұҫПөБРҙр°ёЎҫМвДҝЎҝЎ¶ЦР№ъК«ҙКҙу»бЎ·ТФЎ°ЙНЦР»ӘК«ҙКЈ¬С°ОД»Ҝ»щТтЎўЖ·Йъ»оЦ®ГАЎұОӘ»щұҫЧЪЦјЈ¬БҰЗуНЁ№э¶ФК«ҙКЦӘК¶өДұИЖҙј°ЙНОцЈ¬ҙш¶ҜИ«ГсЦШОВДЗР©ФшҫӯС§№эөД№ЕК«ҙКЈ¬·ЦПнК«ҙКЦ®ГАЈ¬ёРКЬК«ҙКЦ®ИӨЈ¬ҙУ№ЕИЛөДЦЗ»ЫәНЗй»іЦРјіИЎУӘСшЈ¬әӯСшРДБйЈ¬ЧФҝӘІҘТФАҙЙоКЬ№гҙуКҰЙъөДПІ°®Ј¬ДіЦРС§ОӘБЛҪвѧУѧЙъөДК«ҙКЛ®ЖҪЈ¬ҙУ°ЛЎўҫЕДкј¶ёчЛж»ъійИЎБЛ20ГыС§ЙъҪшРРБЛІвКФЈ¬ІўҪ«°ЛЎўҫЕДкј¶ІвКФіЙјЁЈЁ°Щ·ЦЦЖЈ¬өҘО»Јә·ЦЈ©ХыАнИзПВЈә
КХјҜКэҫЭ
°ЛДкј¶ 93 92 84 55 85 82 66 74 88 67 87 87 67 61 87 61 78 57 72 75
ҫЕДкј¶ 68 66 79 92 86 87 61 86 90 83 90 78 70 67 53 79 86 71 61 89
ХыАнКэҫЭ°ҙИзПВ·ЦКэ¶ОХыАнКэҫЭЈ¬ІўІ№И«ұнёсЈә
ІвКФіЙјЁxЈЁ·ЦЈ© | 50ЎЬxЈј60 | 60ЎЬxЈј70 | 70ЎЬxЈј80 | 80ЎЬxЈј90 | 90ЎЬxЎЬ100 |
°Л | 2 | 4 | |||
ҫЕ | 1 | 5 | 5 | 6 | 3 |
ЛөГчЈәІвКФіЙјЁxЈЁ·ЦЈ©Ј¬ЖдЦРxЎЭ80ОӘУЕРгЈ¬70ЎЬxЈј80ОӘБјәГЈ¬60ЎЬxЈј70ОӘәПёсЈ¬0ЎЬxЈј60ОӘІ»әПёсЈ©
·ЦОцКэҫЭІ№И«ПВБРұнёсЦРөДНіјЖБҝЈә
Дкј¶ | ЖҪҫщКэ | ЦРО»Кэ | ЦЪКэ |
°Л | 75.9 | 76.5 | |
ҫЕ | 77.1 | 79 | 86 |
өГіцҪбВЫ
ЈЁ1Ј©ФЪҙЛҙОІвКФЦРЈ¬УРО»Н¬С§өДіЙјЁКЗ78span>·ЦЈ¬ФЪЛыЛщФЪөДДкј¶КфУЪЦРөИЖ«ЙПЈ¬ФтХвО»Н¬С§КфУЪДДёцДкј¶Јҝ
ЈЁ2Ј©ИфҫЕДкј¶УР800ГыС§ЙъЈ¬№АјЖҫЕДкј¶К«ҙКЛ®ЖҪҙпөҪУЕРгөДС§ЙъУР¶аЙЩГыЈҝ