Question

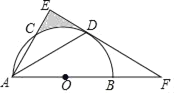
【题目】如图，AB为半圆O的直径，AC是⊙O的一条弦，D为的中点，作DE⊥AC，交AB的延长线于点F，连接DA．

（1）求证：EF为半圆O的切线；

（2）若DA＝DF＝6，求阴影区域的面积．（结果保留根号和π）

Answer 1

【答案】（1）证明见解析 （2）﹣6π

【解析】

（1）直接利用切线的判定方法结合圆心角定理分析得出OD⊥EF，即可得出答案；

（2）直接利用得出S△ACD＝S△COD，再利用S阴影＝S△AED﹣S扇形COD，求出答案．

（1）证明：连接OD，

∵D为弧BC的中点，

∴∠CAD＝∠BAD，

∵OA＝OD，

∴∠BAD＝∠ADO，

∴∠CAD＝∠ADO，

∵DE⊥AC，

∴∠E＝90°，

∴∠CAD+∠EDA＝90°，即∠ADO+∠EDA＝90°，

∴OD⊥EF，

∴EF为半圆O的切线；

（2）解：连接OC与CD，

∵DA＝DF，

∴∠BAD＝∠F，

∴∠BAD＝∠F＝∠CAD，

又∵∠BAD+∠CAD+∠F＝90°，

∴∠F＝30°，∠BAC＝60°，

∵OC＝OA，

∴△AOC为等边三角形，

∴∠AOC＝60°，∠COB＝120°，

∵OD⊥EF，∠F＝30°，

∴∠DOF＝60°，

在Rt△ODF中，DF＝6，

∴OD＝DFtan30°＝6，

在Rt△AED中，DA＝6，∠CAD＝30°，

∴DE＝DAsin30°＝3，EA＝DAcos30°＝9，

∵∠COD＝180°﹣∠AOC﹣∠DOF＝60°，

由CO＝DO，

∴△COD是等边三角形，

∴∠OCD＝60°，

∴∠DCO＝∠AOC＝60°，

∴CD∥AB，

故S△ACD＝S△COD，

∴S阴影＝S△AED﹣S扇形COD＝＝．