题目内容
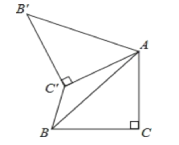
【题目】如图,等边△ABC中,BF是AC边上中线,点D在BF上,连接AD,在AD的右侧作等边△ADE,连接EF,当△AEF周长最小时,∠CFE的大小是( )

A. 30° B. 45° C. 60° D. 90°
【答案】D
【解析】分析:首先证明点E在射线CE上运动(∠ACE=30°),
因为AF为定值,所以当AE+EF最小时,△AEF的周长最小,
作点A关于直线CE的对称点M,连接FM交CE 于E′,此时AE′+FE′的值最小,
根据等边三角形的判定和性质即可求出∠CFE的大小.
详解:∵△ABC,△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=∠ABC=60°,
∴∠BAD=∠CAE,
∴△BAD≌△CAE,
∴∠ABD=∠ACE,
∵AF=CF,
∴∠ABD=∠CBD=∠ACE=30°,
∴点E在射线CE上运动(∠ACE=30°),
作点A关于直线CE的对称点M,连接FM交CE 于E′,此时AE′+FE′的值最小,
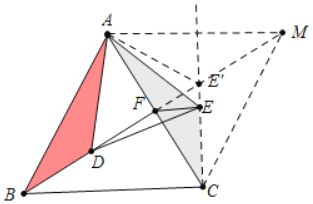
∵CA=CM,∠ACM=60°,
∴△ACM是等边三角形,
∵AF=CF,
∴FM⊥AC,
∴∠CFE′=90°,
故选:D.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
【题目】某商品的定价是每千克5元,元旦期间,该商品推出优惠活动,若一次购买该商品的数量超过2千克,则超过2千克的部分,价格打8折;若一次购买的数量不超过2千克(含2千克),仍按原价付款
(1)根据题意,填写下表
购买的数量(千克) | 1.5 | 2 | 3.5 | 4 | … |
付款金额(元) | 7.5 | 16 | … |
(2)若一次购买的数量为![]() 千克,请你写出付款金额
千克,请你写出付款金额![]() (元)与
(元)与![]() (千克)之间的关系式
(千克)之间的关系式
(3)若某顾客一次购买该商品花费了68元,求该顾客购买商品的数量