��Ŀ����
����Ŀ��ij��˾����һ�����ͽ��ܵ�ˮ�����������ۣ������ڼ׳��к��ҳ���������ͬ�ط�����ͬ���۷����������ۣ��Ա㿪���г��� ��ֻ�ڼ׳������ۣ����ۼ۸�Ϊy��Ԫ/������������Ϊx��������y��x��һ�κ����������
������x������ | 1500 | 2000 |
���ۼ۸�y��Ԫ/���� | 185 | 180 |
�ɱ�Ϊ50Ԫ/�����������۶��٣�ÿ�»���֧������72500Ԫ����������ΪW����Ԫ��
������=���۶�ɱ������ѣ���
��ֻ���ҳ������ۣ����ۼ۸�Ϊ200Ԫ/�����ܸ��ֲ�ȷ������Ӱ�죬�ɱ�ΪaԪ/����aΪ������40��a��70������������Ϊx������ʱ��ÿ�»������ ![]() x2Ԫ�ĸ��ӷѣ���������ΪW����Ԫ��������=���۶�ɱ������ӷѣ���
x2Ԫ�ĸ��ӷѣ���������ΪW����Ԫ��������=���۶�ɱ������ӷѣ���
��1����x=1000ʱ��y��=Ԫ/����w��=Ԫ��
��2���ֱ����W�� �� W����x��ĺ�����ϵʽ������дx��ȡֵ��Χ����
��3����xΪ��ֵʱ���ڼ׳������۵���������������ҳ�����������������ֵ���ڼ׳�����������������ֵ��ͬ����a��ֵ��
��4�����ij��Ҫ��5000����Ʒȫ�������꣬����ͨ�������﹫˾���ߣ�ѡ���ڼ׳��л������ҳ������۲���ʹ����������ϴ�
���𰸡�
��1��190��67500
��2���⣺w��=x��y��50����72500=�� ![]() x2+150x��72500��
x2+150x��72500��
w��=�� ![]() x2+��200��a��x
x2+��200��a��x
��3���⣺��0��x��15000
�൱x=�� ![]() =7500ʱ��w�����
=7500ʱ��w�����
������ã� ![]() =
= 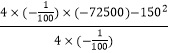 ��
��
���a1=60��a2=340���������⣬��ȥ��������a=60
��4���⣺��x=5000ʱ��w��=427500��w��=��5000a+750000��
��w����w����427500����5000a+750000�����a��64.5��
��w��=w����427500=��5000a+750000�����a=64.5��
��w����w����427500����5000a+750000�����a��64.5��
���ԣ���40��a��64.5ʱ��ѡ���������ۣ�
��a=64.5ʱ���ڼ������۶�һ����
��64.5��a��70ʱ��ѡ���ڼ�����
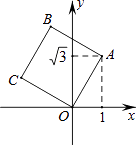
���������⣺��1����y��=kx+b�� ������ ![]() �����
����� 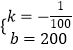 ��
��
��y��=�� ![]() x+200��
x+200��
��x=1000ʱ��y��=190��
w��=x��y��50����72500=�� ![]() x2+150x��72500��
x2+150x��72500��
x=1000ʱ��w��=67500��
�ʴ𰸷ֱ�Ϊ190��67500��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��ij�˶�Ʒ��ר�����������ס��������˶�Ь�����мס��������˶�Ь�Ľ��ۺ��ۼ����±�����֪����60˫�����˶�Ь��50˫�����˶�Ь����10000Ԫ
�˶�Ь�۸� | �� | �� |
���ۣ�Ԫ/˫�� | m | m��20 |
�ۼۣ�Ԫ/˫�� | 240 | 160 |
��1����m��ֵ��
��2��Ҫʹ�����ļס��������˶�Ь��200˫������������=�ۼ۩����ۣ�����21000Ԫ���Ҳ�����22000Ԫ���ʸ�ר�����м��ֽ���������
��3���ڣ�2���������£�ר�����������Լ����˶�Ьÿ˫�Ż�a��50��a��70��Ԫ���ۣ������˶�Ь�۸䣮��ô��ר����Ҫ����������Ӧ��ν�����