题目内容
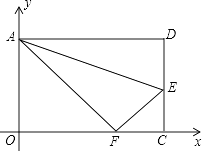
【题目】如图，四边形ABCD与EFGH均为正方形，点B、F在函数y= 
（x＞0）的图象上，点G、C在函数y=﹣ 
（x＜0）的图象上，点A、D在x轴上，点H、E在线段BC上，则点G的纵坐标 ．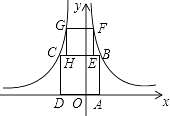 
【答案】
+1
【解析】解：设线段AB的长度为a，线段EF的长度为b（a＞0，b＞0）， 令y= 
（x＞0）中y=a，则x= 
，
即点B的坐标为（ ，a）；
令y=﹣ 
（x＜0）中y=a，则x=﹣ 
，
即点C的坐标为（﹣ ，a）．
∵四边形ABCD为正方形，
∴ ﹣（﹣ ）=a，
解得：a=2，或a=﹣2（舍去）．
令y= （x＞0）中y=2+b，则x= 
，
即点F的坐标为（ ，2+b）；
令y=﹣ （x＜0）中y=2+b，则x=﹣ 
，
即点G的坐标为（﹣ ，2+b）．
∵四边形EFGH为正方形，
∴ +（﹣ ）=b，即b2+2b﹣4=0，
解得：b= ﹣1，或b=﹣ ﹣1（舍去）．
∴a+b=2+ ﹣1= +1．
所以答案是： +1．
【题目】某公司生产一种新型节能电水壶并加以销售，现准备在甲城市和乙城市两个不同地方按不同销售方案进行销售，以便开拓市场． 若只在甲城市销售，销售价格为y（元/件）、月销量为x（件），y是x的一次函数，如表，
月销量x（件） | 1500 | 2000 |
销售价格y（元/件） | 185 | 180 |
成本为50元/件，无论销售多少，每月还需支出广告费72500元，设月利润为W甲（元）
（利润=销售额﹣成本﹣广告费）．
若只在乙城市销售，销售价格为200元/件，受各种不确定因素影响，成本为a元/件（a为常数，40≤a≤70），当月销量为x（件）时，每月还需缴纳 
x2元的附加费，设月利润为W乙（元）（利润=销售额﹣成本﹣附加费）．
（1）当x=1000时，y甲=元/件，w甲=元；
（2）分别求出W甲 ， W乙与x间的函数关系式（不必写x的取值范围）；
（3）当x为何值时，在甲城市销售的月利润最大？若在乙城市销售月利润的最大值与在甲城市销售月利润的最大值相同，求a的值；
（4）如果某月要将5000件产品全部销售完，请你通过分析帮公司决策，选择在甲城市还是在乙城市销售才能使所获月利润较大？
